This is the third and last entry in a series of posts about lattice block reduction. See here and here for the first and second parts, resp. In this post I will assume you have read the other parts.

In the first two parts we looked at BKZ and Slide reduction, the former being the oldest and most useful in practice, while the latter achieves the best provable bounds and has the cleaner analysis. While BKZ is a natural generalization of LLL, we have seen that the analysis of LLL does not generalize well to BKZ. One can view Slide reduction as a different generalization of LLL with the goal of also naturally generalizing its analysis. As we mentioned in the first part, there is another analysis technique based on dynamical systems, introduced in [HPS11]. Unfortunately, as applied to BKZ, there are some cumbersome technicalities and the resulting bounds on the output quality are not as tight as we would like them to be (i.e. as for Slide reduction). One can view the algorithm we are considering today – SDBKZ [MW16] – as a generalization of LLL that lends itself much easier to this dynamical systems analysis: it is simpler, cleaner and yields better results. Since part of the goal of today’s post is to demonstrate this very useful analysis technique, SDBKZ is a natural candidate.

SDBKZ

Recall the two tools we’ve been relying on in the first two algorithms, SVP and DSVP reduction of projected subblocks:

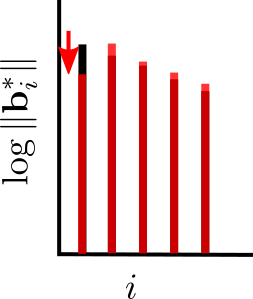
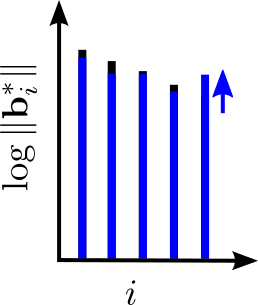
We will use both of them again today. Like BKZ, a tour of SDBKZ starts by calling the SVP oracle on successive blocks of our basis. However, when we reach the end of the basis, we will not decrease the size of the window, since this is actually quite inconvenient for the analysis. Instead, we will keep the size of the window constant but switch to DSVP reduction, i.e. at the end of the BKZ tour we DSVP reduce the last block. This will locally maximize the last GSO vector in the basis, just as the first SVP call locally minimized the first vector of the basis. Then we will move the window successively backwards, mirroring a BKZ tour, but using DSVP reduction, until we reach the beginning of the basis again. At this point, we switch back to SVP reduction and move the window forward, etc. So SDBKZ runs in forward and backward tours.

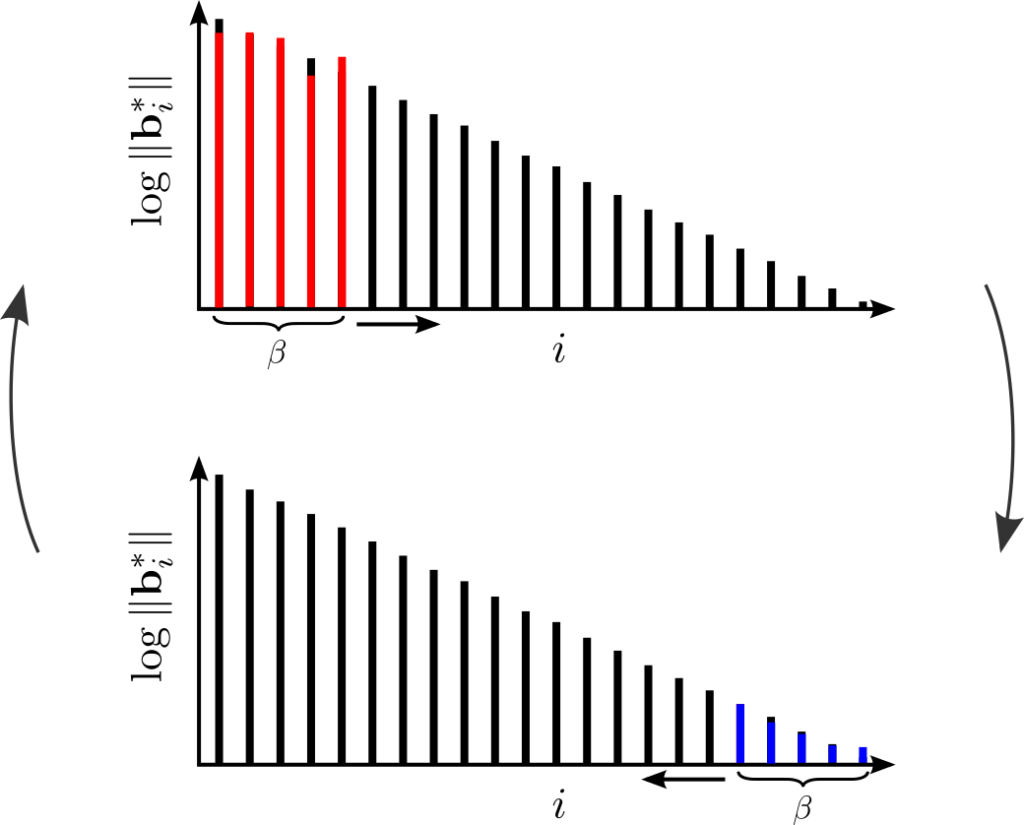
A nice observation here is that the backward tour can be viewed equivalently as: 1) compute the reversed dual basis (i.e. the dual basis with reversed columns), 2) run a forward tour, 3) compute the primal basis again. The first of these two steps is self-inverse: computing the reversed dual basis of the reversed dual basis yields the original primal basis. This means step 3) is actually the same as step 1). So in effect, one can view SDBKZ as simply repeating the following two steps: 1) run a forward tour, 2) compute the reversed dual basis. So it doesn’t matter if we use the primal or the dual basis as input, the operations of the algorithm are the same. This is why it is called Self-Dual BKZ.

There is one caveat with this algorithm: it is not clear, when one should terminate. In BKZ and Slide reduction one can formulate clear criteria, when the algorithm makes no more progress anymore. In SDBKZ this is not the case, but the analysis will show that we can bound the number of required tours ahead of time.

The Analysis

We will start by analyzing the effect of a forward tour. Let \({\mathbf{B}}\) be our input basis. The first call to the SVP oracle in a forward tour replaces \({\mathbf{b}}_1\) with the shortest vector in \({\mathbf{B}}_{[1,k]}\). This means that the new basis \({\mathbf{B}}’\) satifies \(\| {\mathbf{b}}_1′ \| \leq \sqrt{\gamma_k} (\prod_{i=1}^k \|{\mathbf{b}}_i^* \|)^{1/k}\) by Minkowski’s bound. Equivalently, this can be written as \[\log \| {\mathbf{b}}_1′ \| \leq \log \sqrt{\gamma_k} + \frac1k (\sum_{i=1}^k \log \|{\mathbf{b}}_i^* \|).\] So if we consider the \(\log \|{\mathbf{b}}_i^*\|\) as variables, it seems like linear algebra could be useful here. So far, so good. The second step is more tricky though. We know that the next basis \({\mathbf{B}}”\), i.e. after the call to the SVP oracle on \({\mathbf{B}}’_{[2,k+1]}\), satisfies \({\mathbf{b}}_1” = {\mathbf{b}}_1’\) and \(\| ({\mathbf{b}}_2”)^* \| \leq \sqrt{\gamma_k} (\prod_{i=2}^{k+1} \|({\mathbf{b}}’_i)^* \|)^{1/k}\). Unfortunately, we have no control over \(\|({\mathbf{b}}’_i)^* \|\) for \(i \in {2,\dots,k} \), since we do not know how the SVP oracle in the first call changed these vector. However, we do know that the lattice \({\mathbf{B}}_{[1,k+1]}\) did not change in that call. So we can write \[\prod_{i=2}^{k+1} \|({\mathbf{b}}’_i)^* \| = \frac{\prod_{i=1}^{k+1} \|{\mathbf{b}}_i^* \|}{\| {\mathbf{b}}’_1 \|}\] and thus we obtain \[\log \| ({\mathbf{b}}_2′)^* \| \leq \log \sqrt{\gamma_k} + \frac1k (\sum_{i=1}^{k+1} \log \|{\mathbf{b}}_i^* \| – \log \|{\mathbf{b}}’_1 \|).\] Again, this looks fairly “linear algebraicy”, so it could be useful. But there is another issue now: in order to get an inequality purely in the input basis \({\mathbf{B}}\), we would like to use our inequality for \(\log \|{\mathbf{b}}_1′ \|\) in the one for \(\log \| ({\mathbf{b}}_2′)^* \|\). But the coefficient of \(\log \|{\mathbf{b}}_1′ \|\) is negative, so we would need a lower bound for \(\log \|{\mathbf{b}}_1′ \|\). Furthermore, we would like to use upper bounds for our variables later, since the analysis of a tour will result in upper bounds and we would like to apply it iteratively. For this, negative coefficients are a problem. So, we need one more modification: we will use a change of variable to fix this. Instead of considering the variables \(\log \| {\mathbf{b}}_i^* \|\), we let the input variables to our forward tour be \(x_i = \sum_{j < k+i} \log \|{\mathbf{b}}^*_i \|\) and the output variables \(y_i = \sum_{j \leq i} \log \|({\mathbf{b}}’_i)^* \|\) for \(i \in [1,\dots,n-k]\). Clearly, we can now write our upper bound on \(\log \|({\mathbf{b}}’_1)^*\|\) as \[y_1 \leq \log \sqrt{\gamma_k} + \frac{x_1}{k}.\] More generally, we have \[\|({\mathbf{b}}’_i)^* \| \leq \sqrt{\gamma_k} \left(\frac{\prod_{j=1}^{i+k-1} \|{\mathbf{b}}_j^* \|}{\prod_{j=1}^{i-1} \|({\mathbf{b}}’_j)^* \|} \right)^{\frac1k}\] which means for our variables \(x_i\) and \(y_i\) that \[y_i = y_{i-1} + \log \| ({\mathbf{b}}’_i)^* \| \leq y_{i-1} + \log \sqrt{\gamma_k} + \frac{x_i – y_{i-1}}{k} = (1-\frac1k) y_{i-1} + \frac1k x_i + \log \sqrt{\gamma_k}.\]

Note that we can write each \(y_i\) in terms of \(x_i\) and the previous \(y_i\) with only positive coefficients. So now we can apply induction to write each \(y_i\) only in terms of the \(x_i\)’s, which shows that \[y_i = \frac1k \sum_{j=1}^i \omega^{i-j} x_j + (1-\omega)^i k \alpha\] where we simplified notation a little by defining \(\alpha = \log \sqrt{\gamma_k}\) and \(\omega = 1-\frac1k\). By collecting the \(x_i\)’s and \(y_i\)’s in a vector each, we have the vectorial inequality \[{\mathbf{y}} \leq {\mathbf{A}} {\mathbf{x}} + {\mathbf{b}}\] where \[{\mathbf{b}} = \alpha k \left[ \begin{array}{c} 1 – \omega \\ \vdots \\ 1 – \omega^{n-k} \end{array}\right] \qquad\qquad {\mathbf{A}} = \frac1k \left[ \begin{array}{cccc} 1 & & & \\ \omega & 1 & & \\ \vdots & \ddots & \ddots & \\ \omega^{n-k-1} & \cdots & \omega & 1 \end{array} \right].\]

Now recall that after a forward tour, SDBKZ computes the reversed dual basis. Given the close relationship between the primal and the dual basis and their GSO, one can show that simply reversing the vector \({\mathbf{y}}\) will yield the right variables \({\mathbf{x}}’_i\) to start the next “forward tour” (which is actually a backward tour, but on the dual). I.e. after reversing \({\mathbf{y}}\), the variables represent the logarithm of the corresponding subdeterminants of the dual basis. (For this we assume for convenience and w.l.o.g. that the lattice has determinant 1; otherwise, there would be a scaling factor involved in this transformation.)

In summary, the effect on the vector \({\mathbf{x}}\) of executing once the two steps, 1) forward tour and 2) computing the reversed dual basis, can be described as \[{\mathbf{x}}’ \leq {\mathbf{R}} {\mathbf{A}} {\mathbf{x}} + {\mathbf{R}} {\mathbf{b}}\] where \({\mathbf{R}}\) is the reversed identity matrix (i.e. the identity matrix with reversed columns). Iterating the two steps simply means we will be iterating the vectorial inequality above. So analyzing the affine dynamical system \[{\mathbf{x}} \mapsto {\mathbf{R}} {\mathbf{A}} {\mathbf{x}} + {\mathbf{R}} {\mathbf{b}}\] will allow us to deduce information about the basis after a certain number of iterations.

Small Digression: Affine Dynamical Systems

Consider some dynamical system \({\mathbf{x}} \mapsto {\mathbf{A}} {\mathbf{x}} + {\mathbf{b}} \) and assume it has exactly one fixed point, i.e. \({\mathbf{x}}^*\) such that \({\mathbf{A}} {\mathbf{x}}^* + {\mathbf{b}} = {\mathbf{x}}^* \). We can write any input \({\mathbf{x}}’\) as \({\mathbf{x}}’ = {\mathbf{x}}^* + {\mathbf{e}}\) for some “error vector” \({\mathbf{e}}\). When applying the system to it, we get \({\mathbf{x}}’ \mapsto {\mathbf{A}} {\mathbf{x}}’ + {\mathbf{b}} = {\mathbf{x}}^* + {\mathbf{A}} {\mathbf{e}}\). So the error vector \({\mathbf{e}}\) is mapped to \({\mathbf{A}} {\mathbf{e}}\). Applying this \(t\) times maps \({\mathbf{e}}\) to \({\mathbf{A}}^t {\mathbf{e}}\), which means after \(t\) iterations the error vector has norm \(\|{\mathbf{A}}^t {\mathbf{e}} \|_{p} \leq \|{\mathbf{A}}^t \|_{p} \| {\mathbf{e}} \|_{p} \) (where \(\| \cdot \|_{p}\) is the matrix norm induced by the vector \(p\)-norm). If we can show that \(\|{\mathbf{A}} \|_p \leq 1 – \epsilon\), then \(\|{\mathbf{A}}^t \|_p \leq \|A \|^t \leq (1-\epsilon)^t \leq e^{-\epsilon t}\), so the error vector will decay exponentially in \(t\) with base \(e^{-\epsilon}\) and the algorithm converges to the fixed point \({\mathbf{x}}^*\).

Back to our concrete system above. As we just saw, we can analyze its output quality by computing its fixed point and its running time by computing \(\|{\mathbf{R}} {\mathbf{A}} \|_p\) for some induced matrix \(p\)-norm. Since this has been a lenghty post already, I hope you’ll trust me that our system above has a fixed point \({\mathbf{x}}^*\), which can be written out explicitely in closed form. As a teaser, its first coordinate is \[x^*_1 = \frac{(n-k)k}{k-1} \alpha.\] This means that if the algorithm converges, it will converge to a basis such that \(\sum_{j \leq k}\log \| {\mathbf{b}}_j^*\| \leq \frac{(n-k)k}{k-1} \log \sqrt{\gamma_k}\). Applying Minkowski’s Theorem to the first block \({\mathbf{B}}_{[1,k]}\) now shows that the shortest vector in this block satisfies \(\lambda_1({\mathbf{B}}_{[1,k]}) \leq \sqrt{\gamma_k}^{\frac{n-1}{k-1}}\). Note that the next forward tour will find a vector of such length. Recall that we assumed that our lattice has determinant 1, so this is exactly the Hermite factor achieved by Slide reduction, but for arbitrary block size (we do not need to assume that \(k\) divides \(n\)) and better than what we can achieve for BKZ (even using the same technique). Moreover, the fixed point actually gives us more information: the other coordinates (that I have ommited here) allow us control over all but \(k\) GSO vectors and by terminating the algorithm at different positions, it allows us to choose which vectors we want control over.

It remains to show that the algorithm actually converges and figure out how fast. It is fairly straight-forward to show that \[\|{\mathbf{R}} {\mathbf{A}}\|_{\infty} = \|{\mathbf{A}}\|_{\infty} = 1 – \omega^{n-k} \approx e^{-\frac{n-k}{k}}.\] (Consider the last row of \({\mathbf{A}}\).) This is always smaller than 1, so the algorithm does indeed converge. For \(k = \Omega(n)\) this is bounded far enough from 1 such that the system will converge to the fixed point up to an arbitrary constant in a number of SVP calls that is polynomial in \(n\). Using another change of variable [N16] or considering the relative error instead of the absolute error [MW15], one can show that this also holds for smaller \(k\).

As mentioned before, this type of analysis was introduced in [HPS11] and has inspired new ideas even in the heuristic analysis of BKZ. In particular, one can predict the behavior of BKZ by simply running such a dynamical system on typical inputs (and making some heuristic assumptions). This idea has been and is being used extensively in cryptanalysis and in optimizing parameters of state-of-the-art algorithms.

Finally, a few last words on SDBKZ: we have seen that it achieves a good Hermite factor, but what can we say about the approximation factor? I actually do not know if the algorithm achieves a good approximation factor and also do not see a good way to analyze it. However, there is a reduction [L86] from achieving approximation factor \(\alpha\) to achieving Hermite factor \(\sqrt{\alpha}\). So SDBKZ can be used to achieve approximation factor \(\gamma_k^{\frac{n-1}{k-1}}\). This is a little unsatisfactory in two ways: 1) the reduction results in a different algorithm, and 2) the bound is a little worse than the factor achieved by slide reduction, which is \(\gamma_k^{\frac{n-k}{k-1}}\). On a positive note, a recent work [ALNS20] has shown that, due to the strong bound on the Hermite factor, SDBKZ can be used to generalize Slide reduction to arbitrary block size \(k\) in a way to achieve the approximation factor \(\gamma_k^{\frac{n-k}{k-1}}\). Another recent work [ABFKSW20] exploited the fact that SDBKZ allows to heuristically predict large parts of the basis to achieve better bounds on the running time of the SVP oracle.

• Lovász. An Algorithmic Theory of Numbers, Graphs and Convexity. 1986

• Hanrot, Pujol, Stehlé. Analyzing blockwise lattice algorithms using dynamical systems. CRYPTO 2011

• Micciancio, Walter. Practical, predictable lattice basis reduction – Full Version. http://eprint.iacr.org/2015/1123

• Micciancio, Walter. Practical, predictable lattice basis reduction. EUROCRYPT 2016

• Neumaier. Bounding basis reduction properties. Designs, Codes and Cryptography 2016

• Aggarwal, Li, Nguyen, Stephens-Davidowitz. Slide Reduction, Revisited—Filling the Gaps in SVP Approximation. CRYPTO 2020

• Albrecht, Bai, Fouque, Kirchner, Stehlé, Wen. Faster Enumeration-based Lattice Reduction: Root Hermite Factor \(k^{(1/(2k))}\) in Time \(k^{(k/8 + o(k))}\). CRYPTO 2020