By Henry Pfister, Yury Polyanskiy, Rüdiger Urbanke and Yihong Wu

1 Information Theory

The publication of Shannon’s 1948 paper [Sha48] is widely recognized as the inception of information theory as a field of study. A key result in Shannon’s paper is that messages can be transmitted reliably over a noisy channel if and only if a sufficient amount of redundancy is added to correct errors. In particular, the error probability after decoding can be made to vanish as the message length increases if the rate R (i.e., the number of information bits per channel use) is less than the Shannon capacity C of the channel. Shannon’s proof relies on a randomly chosen codebook and does not lend itself to the practical construction of good codes. Thus, the 1948 paper also marks the beginning of the search for deterministic code constructions that achieve the Shannon capacity.

First, we consider a simple model of point-to-point communication. The binary erasure channel is a noisy channel with input alphabet {0, 1} and output alphabet {0, 1, ?}. During each time step, the transmitter sends an arbitrary element of the input alphabet, X, and the receiver observes a random channel output, Y, whose distribution is given by

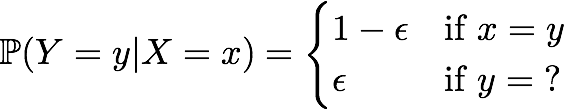
The Shannon capacity of the channel is C = 1 − ϵ bits per channel use.

In wireless networks, the point-to-point model of communication does not capture the true complexity of the problem. One may also consider how much redundancy is required for pairs of transmitters and receivers to communicate reliably when their transmissions interfere with one another. The mathematical model of this problem is known as the interference channel [Car75]. In this case, the challenge is to determine the minimal amount of redundancy that each transmitter must add to their message. Characterizing the capacity region of the interference channel, namely, the set of rate pairs that allow reliable communication, is among the most significant open problems in information theory.

In the two sections below, we will describe recent advances in the understanding of these two problems.

2 Reed-Muller Codes and Capacity

In 1954, Muller introduced a family of binary codes based on evaluating multivariate binary polynomials of bounded degree [Mul54]. Shortly afterwards, Reed described a low-complexity suboptimal decoder for these codes [Ree54]. These codes are now known as Reed-Muller codes and they have many useful properties. One very interesting property of these codes was recently proven by researchers visiting the Simons Institute; namely, that sequences of Reed-Muller codes achieve capacity on the binary erasure channel under maximum-likelihood decoding.

This partly resolves the long-standing open question of whether or not algebraic codes can achieve capacity on fixed channels. For the case of Reed-Muller codes, this result was first explicitly conjectured by Arikan in 2008 [Ari08]. It was also listed by Emmanuel Abbe as an open problem during the 2015 Information Theory Program at the Simons Institute. Just prior to this, Abbe, Shpilka, and Wigderson proved this result for special cases where the rate asymptotically approaches either 0 or 1 [ASW14]. The general solution was found independently by two groups of researchers visiting the institute: (i) Santhosh Kumar and Henry D. Pfister [KP15] and (ii) Shrinivas Kudekar, Marco Mondelli, Eren Şaşoğlu, and Rüdiger Urbanke [KMŞU15].

One very surprising part of the result is that the proof depends only weakly on the precise structure of Reed-Muller codes. In fact, the proof applies to any sequence of codes where the automorphism group of each code is doubly transitive. This includes primitive narrow-sense BCH codes, quadratic residue codes, and all other affine-invariant codes.

Another surprising part of the proof is that it combines celebrated results from three distinct fields. From computer science, it draws on the deep result of Friedgut and Kalai that symmetric monotone boolean functions have sharp thresholds [FK96]. From information theory, it applies the elegant area theorem for extrinsic information transfer functions [AKB04] which says that the bit erasure rate of the code (as a function of the channel erasure probability ϵ) must satisfy an integral conservation law. From algebraic coding theory, it uses the fact that the automorphism group of a Reed-Muller code contains a doubly transitive subgroup [KLP68]. These results can be combined to show that, for any δ > 0, the bit erasure rate of a length-N Reed-Muller code must transition from δ to 1−δ over an ϵ-range of order 1/log(N). For a sequence of Reed-Muller codes of increasing length whose rates converge to R ∈ (0, 1), this implies that the sequence achieves capacity.

The Simons Institute hosts programs that encourage researchers in theoretical computer science to interact with researchers in other fields and it is indeed apropos that such a combination would be discovered here. It is also amusing to note that Muller found a deterministic construction of capacity achieving codes only 6 years after Shannon’s paper but we didn’t know this for another 60 years.

3 The Gaussian Interference Channel and Costa’s Conjecture

A particular implication of Shannon’s paper [Sha48] is the following result. Let x be a point on the sphere of radius √n inside the Euclidean space ℝⁿ and consider a noisy observation of x:

where Z is standard Gaussian. Using probabilistic methods, Shannon demonstrated that there exists a subset C (called a code) of the sphere such that when x ∈ C is selected uniformly at random, observing Y is sufficient to reconstruct the original x with vanishing probability of error as n → ∞. Most importantly, the size of the code is |C| = exp{nC(γ) + o(n)}, where the exponent C(γ) ≜ ½ log(1 + γ), called capacity, cannot be improved. Practically, the parameter n denotes the transmission time and points of C correspond to different user messages. The capacity C(γ) denotes the maximal rate at which data can be communicated reliably across the noisy channel. Implications of Shannon’s result are thus far-reaching and underpin the majority of modern communication systems: cell phones, cable and satellite TV, computer networks, etc.

In many cases (notably wireless networks) the above additive-noise model is too simplistic to capture the communication systems in reality. Indeed, multiple pairs of transmitter-receivers may occupy the same frequency band and their observations thus become entangled. This is captured by the model of Gaussian interference channel, of which the simplest version is the following:

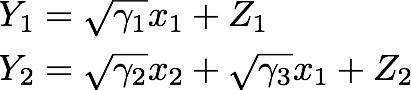
where Z₁,Z₂ are standard Gaussian noise. Despite consistent effort and recent advances, the capacity region of the interference channel, i.e., the set of all achievable rate pairs of the two users, remains generally unknown. A special point (known as the corner point) of the capacity region is the maximal communication rate for the first user when the second user insists on transmitting at its maximal (i.e., interference-free) rate of R₂ = C(γ₂) as in (1). Carleial [Car75] observed that it is possible for the first user to achieve positive communication rate R₁ = C (^γ3/_1+γ2). M. Costa conjectured in [Cos85] that this is in fact optimal.

At the invitation of Chandra Nair, participants of the Simons Institute’s program on Information Theory, Yury Polyanskiy and Yihong Wu, were finally able to prove Costa’s conjecture [PW15]. Their approach was to first apply the transportation-information inequality of Talagrand [Tal96] to reduce the question to studying continuity of entropy with respect to a so-called Wasserstein distance from optimal transportation [Vil08]. Then by a careful analytic estimate they showed that the entropy is O(√n)-Lipschitz in this distance. One interesting feature of the proof is that it does not follow the standard program of “single-letterizing” Fano’s inequality – a technique responsible for virtually all known tight impossibility bounds in information theory [CT06, Chapter 15]. It is exciting, thus, to see in what other contexts this new technique will be applicable.

References