Indistinguishability Obfuscation and Multi-linear Maps: A Brave New World (Guest Post by Ran Canetti)

Posted on by
2

The following post is written by Ran Canetti

A bunch of us hapless cryptographers got the following boilerplate comment from the FOCS’15 PC:

Overall, submissions related to multi-linear maps and indistinguishability obfuscation were held to a somewhat higher standard. The PC expressed some concern with the recent flurry of activities pertaining to multi-linear maps and indistinguishability obfuscation, given how little we understand and can say and *prove* about the underlying hardness assumptions.

This comment was clearly written with the best of intentions, to explain views expressed at the PC deliberations. And I’m thankful to it – mainly since it made the underlying misconceptions so explicit that it mandated a response. So, after discussing and commiserating with colleagues here at Simons, and after amusing ourselves with some analogues of above statement (e.g., “results on NP completeness are held to a higher standard given how little we understand and can say and *prove* about the hardness solving SAT in polynomial time”), I decided to try to write an – obviously subjective – account for the recent developments in multilinear maps and indistinguishability obfuscation (IO) and why this exciting research should be embraced and highlighted rather than “held to a somewhat higher standard” — in spite of how little we understand about the underlying assumptions. The account is aimed at the general CS-theorist.

Let me start by giving rough definitions of the concepts involved. An Indistinguishability Obfuscator (IO) is a randomized algorithm O that takes as input a circuit C and outputs a (distribution over) circuits O(C) with the properties that:

  • C and O(C) have the same functionality,
  • O(C) is only polynomially larger than C,
  • for any two same-size, functionally equivalent circuits C and C’ we have that O(C) ~ O(C’) (i.e., the distributions over strings representing O(C) and O(C’) are computationally indistinguishable).

IO has been proposed as a notion of obfuscation in 2000 (Hada, Barak-Goldreich-Impagliazzo-Sahai-Vadhan-Yang). Indeed, it is arguably a clean and appealing notion – in some sense the natural extension of semantic security of standard encryption to “functionality-preserving encryption of programs”. However, it has been largely viewed as too weak to be of real applicability or interest. (There were also no candidate polytime IO schemes, but this in my eyes is a secondary point, see below.)

Things changed dramatically in 2013 when Sahai and Waters demonstrated how IO schemes can be ingeniously combined with other rather “mundane” cryptographic constructs to do some amazing things. Since then dozens of papers came about that extend the SW techniques and apply them to obtain even more amazing things – that by now have transcended crypto and spilled over to other areas. (e.g.: deniable encryption, succinct delegation, succinct multi-party computation with hardly any interaction, one message succinct witness hiding and witness indistinguishable proofs, hash functions with random-oracle-like properties, hardness results for PPAD, and many more). In fact, think about a result in your area that assumes that some computation is done inside a black box – most probably IO can replace that assumption in one way or another…

Still, my (subjective but distinct) feeling is that we are far from understanding the limits and full power of IO. Furthermore, the study of IO has brought with it a whole new toolbox of techniques that are intriguing in their own right, and teach us about the power and limitations of working with “encrypted computations”.

So far I have not mentioned any candidate constructions of IO – and indeed the above study is arguably valuable as a pure study of this amazing concept, even without any candidate constructions. (Paraphrasing Levin on quantum computers, one can take the viewpoint that the above is the study of impossibility results for IO…)

However, unlike quantum computers, here we also have candidate constructions. This is where multilinear maps come to play.

Multi-linear maps are this cool new technical tool (or set of tools) that was recently put forth. (The general concept was proposed by Boneh and Silverberg around 2000, and the first candidate construction of one of the current variants was presented in 2012 by Garg, Gentry and Halevi.) Essentially, a multilinear map scheme is a fully homomorphic encryption scheme where the public key provides, in addition to the ability to encrypt elements and perform homomorphic operations on ciphertexts, also the ability to partially decrypt ciphertexts under certain restrictions. There are many incomparable variants of this general paradigm, which differ both in the functionality provided and in the security guarantees. Indeed, variants appear to be closely tied to candidate constructions. Furthermore, our understanding of what’s possible here has been evolving considerably, with multiple new constructions, attacks, and fixes reported.
Still, the number and variety of applications of multi-linear maps makes it clear that this “family of primitives” is extremely powerful and well worth studying – both at the level of candidate constructions, at the level of finding the “right” computational abstractions, and at the level of applications. In a sense, we are here back to the 70’s: we are faced with this new set of algebraic and number theoretic tools, and are struggling to find good ways to use them and abstract them.

Indeed, some of the most powerful applications of multilinear maps are candidate constructions of IO schemes. The first such candidate construction (by Garg, Gentry, Halevi, Raykova, Sahai and Waters in 2013) came with only heuristic arguments for security; However more rigorous analyses of this and other constructions, based on well-defined formulations of multi-linear map variants, soon followed suite. Some of these analyses have eventually been “broken” in the sense that we currently don’t have candidate constructions that satisfy the properties they assume. Still, other analyses do remain valid. Indeed, there are no attacks against the actual basic IO scheme of Garg etal.

The fact that the only current candidate constructions of IO need to assume existence of some variant of multi-linear maps at some point or another may make it seem as it the two concepts are somehow tied together. However, there is no reason to believe that this is the case. For all we know, multi-linear maps are just the path first uncovered to IO, and other paths may well be found. Similarly, even if IO turns out to be unobtainable for some reason, the study of multilinear maps and their power will still remain very relevant.

So, to sum up this long-winded account:

  • IO is a natural and fascinating computational concept. Studying its consequences (both within and outside cryptography) is a well worth endeavor.
  • Studying new candidate constructions of IO and/or new analyses of their security is another well worth endeavor.
  • Multilinear maps are an intriguing and powerful set of techniques and tools. Finding better candidate constructions and abstractions is of central importance to cryptography. Finding new cool uses of these maps is another intriguing challenge.
  • The three should be treated as separate (although touching and potentially interleaving) research efforts.

———–
I’d like to thank Guy Rothblum and Vinod Vaikuntanathan for great comments that significantly improved this post.

Historical talks

Posted on by
Reply

During the summer program on cryptography, every Monday afternoon there is a talk on the history of a classic paper or series of papers. Last week, Russell Impagliazzo spoke on his work with Steven Rudich on the impossibility of basing one-way permutations or key agreement on the existence of one-way functions. The week before, Umesh Vazirani spoke on quantum computing, and earlier Ron Rivest spoke about the origins of modern cryptography.

All talks are recorded, and the recordings are available here.

Tomorrow afternoon, Daniele Micciancio will speak at 3pm on lattice-based cryptography.

Tomorrow is also the first day of the Workshop on the mathematics of modern cryptography. The program starts at 9:30am Pacific time, and all talk are broadcast live, as usual.

Tune in at 9:30am (12:30pm Eastern)

Posted on by
Reply

This Summer, most of the theory of cryptography community is in Berkeley to participate in the Simons Institute program on cryptography.

The program started with week-long series of lectures, all available here, which covered tools such as lattice problems, multilinear maps, oblivious RAMs, scrambled circuits, and differential privacy, and their applications to homomorphic encryption, obfuscation, delegated computations, and multiparty computations.

This week there is a workshop on secure computations, all whose talks are livestreamed, which starts today at 9:30 Pacific Time with a talk by Amit Sahai on obfuscation.

Research Vignette: Semialgebraic Geometry of Ranks

Posted on by
Reply

By Kaie Kubjas

The rank of a matrix M is a fundamental notion in linear algebra. While usually defined as the dimension of the span of the rows or the span of the columns, it could also be defined as the minimal number r such that the matrix M admits a factorization as M=AB, where A has r columns and B has r rows. If all entries of the matrix M are nonnegative, then such a factorization can be pictured as a pair of nested polytopes: the outer one is given by the inequalities Ax≥0, and the inner one by the convex hull of the columns of B. Up to an affine transformation, this picture is independent of the specific factorization AB.

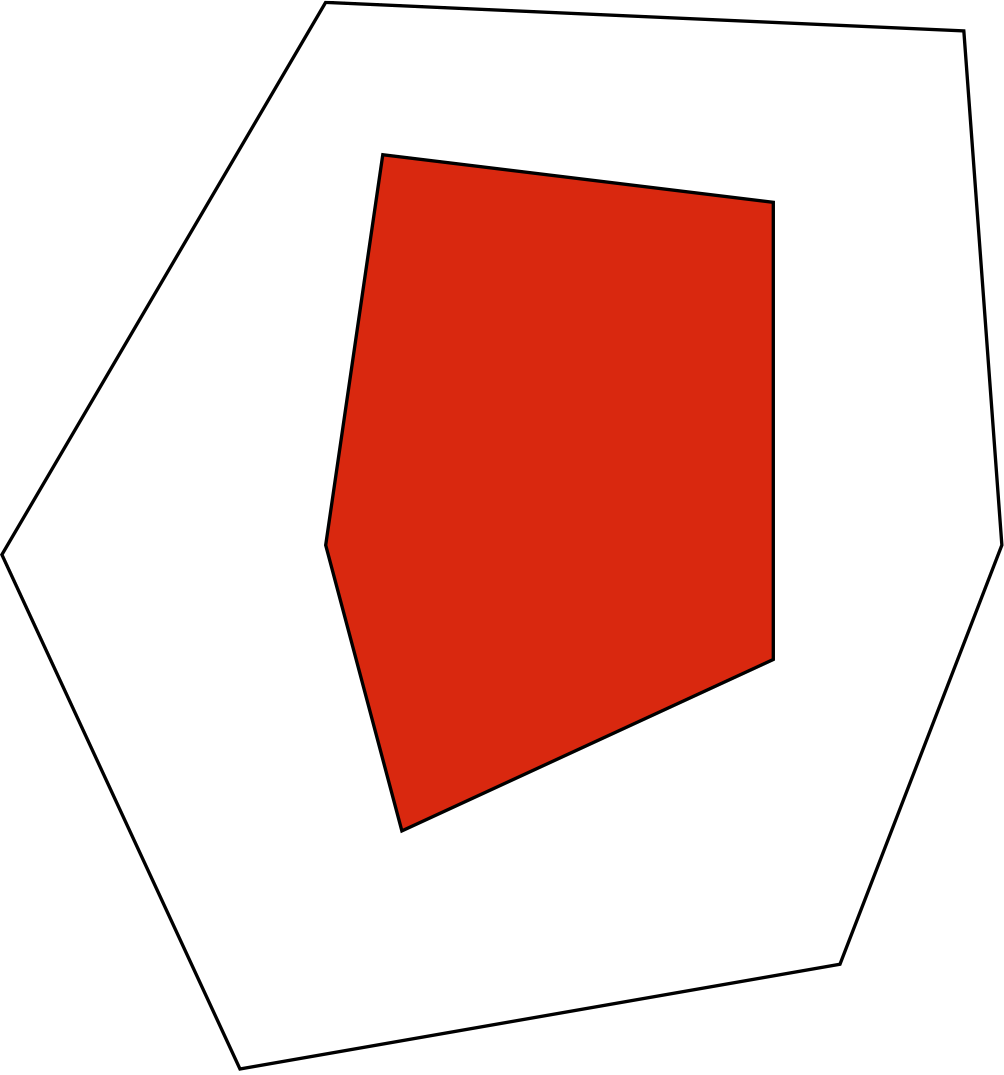Figure 1: Two nested polygons corresponding to a rank 3 matrix with 6 rows and 5 columns

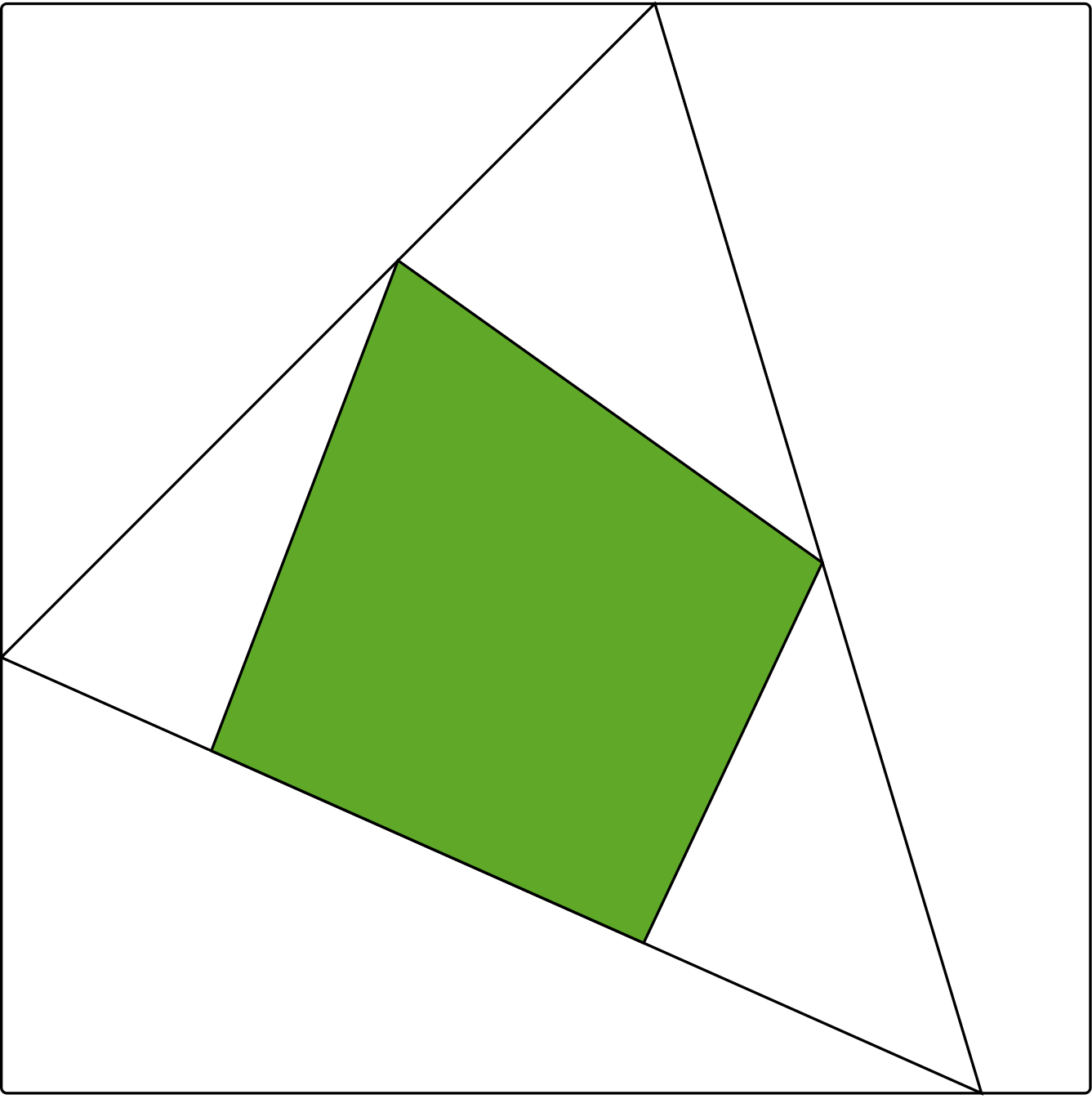In many applications, we are interested in factorizations of a certain particular form. For example, we can study factorizations M=AB where A,B have nonnegative entries. The minimal r as above for which such a factorization exists is called the nonnegative rank. Cohen and Rothblum formulated this definition geometrically: a nonnegative matrix M has nonnegative rank at most r if and only if there exists a polytope with r vertices that can be fitted between two nested polytopes associated with the matrix.

Figure 2: Two quadrangles and a triangle between them

The interest in the nonnegative rank started in the combinatorial optimization community with the work of Yannakakis at the end of the 1980s. A linear program aims to minimize or maximize a linear function over a region that is given by linear constraints, i.e., a polyhedron or a polytope. Yannakakis showed that the minimal number of variables and constraints needed to express a linear program over a polytope is closely related to the nonnegative rank of a matrix associated to this polytope. 

One line of research that started with the seminal paper of Yannakakis studies lower bounds on the nonnegative rank, and later also on the positive semidefinite rank, for different polytopes that appear in combinatorial optimization. For example, the Traveling Salesman Problem (TSP) asks: Given a list of cities, what is the shortest cycle that visits every city exactly once? It can be formulated as a linear program over a region which is called the TSP polytope. The TSP problem is NP-hard, and some of the attempts to prove P=NP aimed to give polynomial formulations of the TSP polytope. This motivated Yannakakis to look for superpolynomial lower bounds on the nonnegative rank of the TSP polytope, which was completed by Fiorini et al. in 2012.

The notion of nonnegative rank also appears in statistics: The set of stochastic matrices of nonnegative rank at most r is called the r-th mixture model. It represents the joint probabilities of two random variables that are independent given a third random variable with r possible values. Given a data matrix that is obtained by an opinion poll or a measurement, one would like to estimate the parameters of the true probability distribution that the data come from. Specifically, the maximum likelihood estimate of a data matrix is a matrix in the r-th mixture model that maximizes a specific function, called the likelihood function. There are several ways for numerically solving the maximum likelihood estimation in practice. These methods, however, do not provide a certificate for having found the global optimum.

In my recent research together with Eggermont, Horobeţ, Robeva, and Sturmfels (Robeva and Sturmfels attended the Algebraic Geometry program, and Horobeţ participated in one of the workshops at the Simons Insitute), we have been interested in exact descriptions of the sets of matrices of nonnegative rank at most r. They are semialgebraic sets, which means that they can be characterized by Boolean combinations of polynomial equations and inequalities. Knowing quantifier-free semialgebraic descriptions of these sets would give an exact method for checking if a matrix lies in them. It would be also an essential step towards computing maximum likelihood estimates with certificate.

CONTINUE READING

Research Vignette: Faster Algorithms for Linear Programming

Posted on by
Reply

By Yin Tat Lee and Aaron Sidford

Interior Point Methods and Algorithmic Spectral Graph Theory

Linear programming has long stood as one of the key pillars of computer science. In practice, problems are often reformulated as linear programs to take advantage of fast implementations of linear programming algorithms. And in theory, the best running times for solving many problems are achieved by using the theoretical guarantees of these algorithms. Moreover, new algorithms for linear programming have tended to cause ripples across the field, yielding not just faster running times but new algorithmic frameworks and a new lens on the structure of difficult problems.

Recently, state-of-the-art linear programming techniques known as interior point methods have been making waves in the area of Algorithmic Spectral Graph Theory, which uses linear algebraic properties of graphs to improve algorithm design. Like many iterative methods for optimization, interior point methods reduce solving difficult problems, like linear programming, to solving a sequence of simpler problems — in this case, solving a system of linear equations. When solving classic network optimization problems like maximum flow and minimum cost flow using interior point algorithms, these linear systems are highly structured. To solve them, it suffices to solve linear systems in the combinatorial Laplacian of a graph, one of the central mathematical objects in spectral graph theory. Consequently, standard interior point methods provide an algorithmic framework that naturally facilitates the leveraging of spectral properties of graphs to obtain fast running times for network optimization problems.

Over the past decade, studying such problems at this boundary of continuous and discrete optimization has been an incredibly fruitful area of research. Building off work of Vaidya in 1991, in 2004 Spielman and Teng produced the first algorithm to solve these Laplacian systems in time nearly-linear in the size of the associated graph. This result influenced a decade of research in algorithmic spectral graph theory, prompted numerous breakthroughs in combinatorial optimization, and ultimately helped inspire much of the research in the Simons Institute’s Fall 2014 program on Algorithmic Spectral Graph Theory.

Moreover, Spielman and Teng’s result implied that iterations of standard interior point methods can be implemented in nearly linear time when solving common network optimization problems. In 2008, Daitch and Spielman proved that such an algorithm not only nearly matches the running time of the state-of-the-art 1998 algorithm of Goldberg and Rao for solving the maximum flow problem, but actually improves upon the previous best known algorithms for solving the minimum cost flow problem. Even more excitingly, over the past two years, modified interior point schemes and fast Laplacian system solvers have been used to improve the running time for exactly solving the maximum flow problem. In 2013, Aleksander Madry provided a faster algorithm for solving sparse unit capacity instances of maximum flow, and in 2014 we provided a new interior point scheme with a faster convergence rate that yielded faster algorithms for solving dense instances of the maximum flow and the minimum cost flow problems.

This interplay between algorithms for continuous optimization and the discrete structure of graphs was one of the central themes of the Simons Institute’s Fall 2014 Program on Algorithmic Spectral Graph Theory. Interior point methods and fast Laplacian system solvers are simply one illustration. Both in recent years and during the program there has been extensive work on using new iterative machinery and new structural properties of graphs to design faster and better algorithms for solving various graph problems. During the semester we enjoyed exploring multiple research questions in this direction and discussing the exciting work of visitors and long term participants. In the remainder of this vignette we will discuss one recent success story in this line of work.

CONTINUE READING