Tag Archives: Lattice Block Reduction

Lattice Blog Reduction – Part II: Slide Reduction

Posted on by
1

This is the second entry in a series of posts about lattice block reduction. See here for the first part. In this post I will assume you have read the first one, so if you haven’t, continue at your own risk. (I suggest reading at least the first part for context, notations and disclaimers.)

Last time we focused on BKZ which applies SVP reduction to successive projected subblocks. In this post we consider slide reduction, which allows for a much cleaner and nicer analysis. But before we can do that, we need a little more background.

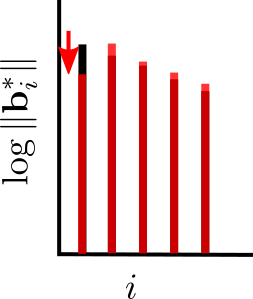
A New Tool: Dual SVP Reduction

As you hopefully know, duality is a very useful concept in lattice theory (and in mathematics more generally). It allows to pair up lattices, which are related in a well defined way. Similarly, we can pair up the different bases of two dual lattices to obtain dual bases. I’ll skip the definition of these two concepts since we will not need them. It is sufficient to know that we can compute the dual basis from the primal basis efficiently. One very cool feature of dual bases is that the last vector in the dual basis has a length that is inverse to the length of the last GSO vector of the primal basis. In math: if \({\mathbf{B}}\) and \({\mathbf{D}}\) are dual bases, then \(\| {\mathbf{b}}_n^* \| = \| {\mathbf{d}}_n \|^{-1}\). (If you want to see why this is true at least for full rank lattices, use the fact that in this case \({\mathbf{D}} = {\mathbf{B}}^{-T}\), and the QR-factorization.) It follows that if \({\mathbf{d}}_n\) happens to be the shortest vector in the dual lattice, then \({\mathbf{b}}_n^*\) is as long as possible, since the existence of any basis \(\bar{{\mathbf{B}}}\) where \(\|\bar{{\mathbf{b}}}_n^*\| > \|{\mathbf{b}}_n^*\|\) would imply that there exists a dual basis \(\bar {{\mathbf{D}}}\) such that \(\| \bar{{\mathbf{d}}}_n\| < \| {\mathbf{d}}_n\| \). By analogy to SVP reduction, we call a basis, where \(\| {\mathbf{b}}^*_n \|\) is maximized, dual SVP reduced (DSVP reduced). This gives us a new tool to control the size of the GSO vectors: we can apply an SVP algorithm to the dual basis of a projected subblock \({\mathbf{B}}_{[i,j]}\). This will yield a shortest vector in the dual of this projected sublattice. Then we can compute a dual basis, which contains this shortest vector in the last position and finally compute a new primal basis for this projected subblock, which now locally maximizes \(\|{\mathbf{b}}_j^* \|\). As we did for primal SVP reduction in the last post, we will assume access to an algorithm that, given a basis \({\mathbf{B}}\) and indices \(i,j\), will return a basis such that \({\mathbf{B}}_{[i,j]}\) is DSVP reduced and the rest of the basis is unchanged. We will call such an algorithm a DSVP oracle. It may sound like this should be somewhat less efficient than SVP reduction, since we have to switch between the dual and the primal bases (which, when done explicitly, requires matrix inversion), but this is not actually the case. In fact, one can implement a DSVP reduction entirely without having to explicitly compute (any part of) the dual basis as shown in [GN08,MW16].

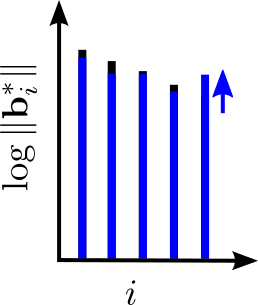
Effect of a call to the DSVP oracle. GSO log norms of the input in black, of the output in blue. Note that the sum of the GSO log norms is a constant, so increasing the length of the last vector, decreases the (average of the) remaining vectors.

I hope this figure provides some intuition that such an oracle can be useful. Now let us quantify how much this DSVP oracle helps us. Recall that in the primal SVP reduction we used Minkowski’s theorem to bound the length of the first vector. Since we are now applying the SVP algorithm to the dual, it should come as no surprise that we will use Minkowski’s theorem on the dual lattice, which tells us that \[\lambda_1(\widehat{\Lambda}) \leq \sqrt{\gamma_n} \det(\widehat{\Lambda})^{1/n} = \sqrt{\gamma_n} \det(\Lambda)^{-1/n}\] where \(\widehat{\Lambda}\) is the dual lattice, i.e. the lattice generated by the dual basis. Furthermore, by exploiting above fact that for basis \({\mathbf{B}}\) and its dual \({\mathbf{D}}\) we have \(\| {\mathbf{b}}_n^* \| = \|{\mathbf{d}}_n \|^{-1}\), this shows that if \({\mathbf{B}}\) is DSVP reduced, i.e. \({\mathbf{d}}_n\) is a shortest vector in the dual lattice, then \[\| {\mathbf{b}}_n^* \| = \|{\mathbf{d}}_n \|^{-1} = \lambda_1(\widehat{\Lambda})^{-1} \geq \frac{\det(\Lambda)^{1/n}}{\sqrt{\gamma_n}}.\] So after we’ve applied the DSVP oracle to a projected block \({\mathbf{B}}_{[i-k+1,i]}\), we have \[\|{\mathbf{b}}^*_i \| \geq \frac{\left(\prod_{j = i-k+1}^{i} \|{\mathbf{b}}_j^* \| \right)^{1/k}}{\sqrt{\gamma_{k}}}.\]

Slide Reduction

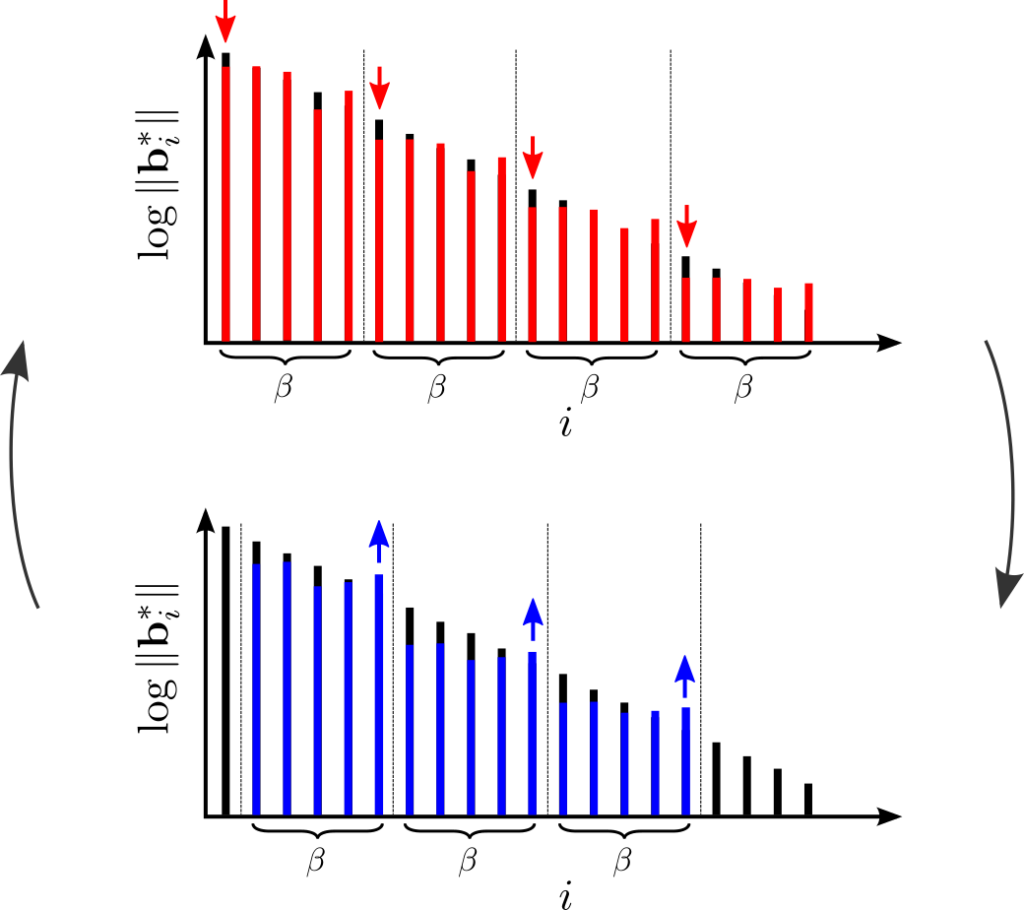
Now we have all the tools we need to describe slide reduction [GN08]. One of the major hurdles to apply an LLL-style running time analysis to BKZ seems to be that the projected subblocks considered in that algorithm are maximally overlapping. So slide reduction takes a different route: it applies primal and dual SVP reduction to minimally overlapping subblocks, which allows to still prove nice bounds on the output quality (in fact, even better than BKZ), but also on the running time via a generalization of the LLL analysis. More specifically, let \({\mathbf{B}}\) be the given lattice basis of an \(n\)-dimensional lattice and \(k\) be the blocksize. We require that \(k\) divides \(n\). (We’ll come back to that restriction later.) Instead of applying our given SVP oracle to successive projected subblocks, we apply it to disjoint projected subblocks, i.e. to the blocks \({\mathbf{B}}_{[1,k]}\), \({\mathbf{B}}_{[k+1,2k]}\), etc. So we locally minimize the GSO vectors \({\mathbf{b}}^*_{ik + 1}\) for \(i \in \{0,\cdots,n/k – 1\}\). (Technically, we iterate this step with a subsequent LLL reduction until there is no more change, which is important for the runtime analysis, but let’s ignore this for now). So now we have a basis where these disjoint projected subblocks are SVP-reduced. In the next step we shift the blocks by 1 and apply our DSVP oracle to them. (Note that the last block now extends beyond the basis, so we ignore this block.) This has the effect of locally maximizing the vectors \({\mathbf{b}}^*_{ik + 1}\) for \(i \in \{1,\cdots,n/k – 1\}\). This might seem counter-intuitive at first, but note that the optimization context for \({\mathbf{b}}^*_{ik + 1}\) changes between the SVP reduction and the DSVP reduction: \({\mathbf{b}}^*_{ik + 1}\) is first minimized with respect to the block \({\mathbf{B}}_{[ik+1,(i+1)k]}\) and then maximized with respect to the block \({\mathbf{B}}_{[(i-1)k+1,ik+1]}\). So one can view this as using the block \({\mathbf{B}}_{[ik+2, (i+1)k]}\) as a pivot to lower the ratio between the lengths of the GSO vectors \({\mathbf{b}}^*_{ik+1}\) and \({\mathbf{b}}^*_{(i+1)k+1}\). This view is reminiscent of the proof of Mordell’s inequality \(\gamma_n^{\frac{1}{n-1}} \leq \gamma_{n-1}^{\frac{1}{n-2}}\), which explains the title of the paper [GN08]. The idea of slide reduction is to simply iterate these two steps until there is no more change.

Slide reduction in one picture: apply the SVP oracle to the disjoint projected blocks in parallel, then shift the blocks by 1 and apply the DSVP oracle. Repeat.

Let’s dive into the analysis.

The Good

When the algorithm terminates, we are guaranteed that the following conditions hold simultaneously:

  1. The blocks \({\mathbf{B}}_{[ik+1, (i+1)k]}\) are SVP reduced for all \(i \in \{0,\cdots,n/k – 1\}\) (the primal conditions), which implies \[\|{\mathbf{b}}^*_{ik+1} \|^{k-1} \leq \gamma_k^{k/2} \prod_{j=ik+2}^{(i+1)k} \|{\mathbf{b}}^*_j \|\] (Note that we raised Minowski’s bound to the \(k\)-th power and canceled one the \(\|{\mathbf{b}}^*_{ik+1} \|\) on both sides.)

  2. The blocks \({\mathbf{B}}_{[ik+2, (i+1)k+1]}\) are DSVP reduced for all \(i \in \{0,\cdots,n/k – 2\}\) (the dual conditions), which implies \[\gamma_{k}^{k/2} \|{\mathbf{b}}^*_{(i+1)k+1} \|^{k-1} \geq \prod_{j = ik+2}^{(i+1)k} \|{\mathbf{b}}_j^* \|\]

(Technically, there is a constant slack factor \(>1\) involved, which can be set arbitrarly close to 1, but is important for running time. We’ll sweep under the rug for simplicity.)

Just by staring at the two inequalities, you will notice that they can easily be combined to yield: \[\|{\mathbf{b}}^*_{ik+1} \| \leq \gamma_k^{\frac{k}{k-1}} \|{\mathbf{b}}^*_{(i+1)k+1} \|\] for all \(i \in \{0,\dots,n/k-2\}\) and in particular \[\|{\mathbf{b}}^*_{1} \| \leq \gamma_k^{\frac{k}{k-1} (\frac{n}{k}-1)} \|{\mathbf{b}}^*_{n-k+1} \| = \gamma_k^{\frac{n-k}{k-1}} \|{\mathbf{b}}^*_{n-k+1} \|\] By a similar trick as last time we can assume that \(\lambda_1({\mathbf{B}}) \geq \|{\mathbf{b}}^*_{n-k+1} \|\), because the last block is SVP-reduced, which shows that slide reduction achieves an approximation factor \[\|{\mathbf{b}}^*_{1} \| \leq \gamma_k^{\frac{n-k}{k-1}} \lambda_1({\mathbf{B}}).\] Done! Yes, it is really that simple. With (very) little more work one can similarly show a bound on the Hermite factor \[\|{\mathbf{b}}^*_{1} \| \leq \gamma_k^{\frac{n-1}{2(k-1)}} \det({\mathbf{B}})^{\frac1n}.\] Simply reuse the bounds on the ratios of \(\| {\mathbf{b}}^*_1 \|\) and \(\| {\mathbf{b}}^*_{ik+1} \|\) in combination with Minkowski’s bound for each block. (You guessed it: Homework!) Note that both of them are better than what we were able to obtain for BKZ in our last blog post. And in contrast to BKZ one can easily bound the number of calls to the SVP oracle by a polynomial in \(n, k\) and the bit size of the original basis. The analysis is similar to the one of LLL with a modified potential function: we let \(P({\mathbf{B}}) = \prod_{i=0}^{n/k-2} \det({\mathbf{B}}_{[1,ik]})^2\). If the basis \({\mathbf{B}}\) consists of integer coefficients only, this potential is also integral. Furthermore, one can show that if an iteration of slide reduction modifies the basis, it will decrease this potential by at least a constant factor (by using the slack factor we brushed over). This shows that while the basis is modified, the potential decreases exponentially, which results in a polynomial number of calls to the (D)SVP oracle.

The Bad

We just sketched a complete and elegant analysis of the entire algorithm and it checks all the boxes: best known approximation factor, best known Hermite factor, a polynomial number of calls to its (D)SVP oracle. So what could possibly be bad about it? Remember that we required that the blocksize \(k\) divides the dimension \(n\). It seems like it should be easy to get rid of this restriction, for example one could artificially increase the dimension of the lattice to assure that the blocksize divides it. Unfortunately, this and similar approaches will degrade the bound on the output quality – there will be a rounding-up operator in the exponent [LW13]. For small \(k\) this might not be too much of an issue, but as \(k\) grows, this results in a significant performance hit. Luckily, a recent work [ALNS19] shows that one can avoid this degradation by combining slide reduction with yet another block reduction algorithm: SDBKZ, which will be the topic of the next post.

The Ugly

Slide reduction is beautiful and there is little one can find ugly about it in theory. Unfortunately, experimental studies so far concluded that this algorithm is significantly inferior to BKZ, which (at least to me) is puzzling. This is often attributed to the fact that BKZ uses maximally overlapping blocks, which seems to allow it to obtain stronger reduction notions (even though we cannot prove it). So, one could wonder if there is an algorithm that uses maximally overlapping blocks (and is thus hopefully competetive in practice), but allows for a clean analysis. It turns out that the topic of the next post (SDBKZ) is such an algorithm.

  • Gama, Nguyen. Finding short lattice vectors within Mordell’s inequality. STOC 2008

  • Li, Wei. Slide reduction, successive minima and several applications. Bulletin of the Australian Mathematical Society 2013

  • Micciancio, Walter. Practical, predictable lattice basis reduction. EUROCRYPT 2016

  • Aggarwal, Li, Nguyen, Stephens-Davidowitz. Slide Reduction, Revisited—Filling the Gaps in SVP Approximation. https://arxiv.org/abs/1908.03724

Lattice Blog Reduction – Part I: BKZ

Posted on by
3

This is the first entry in a (planned) series of at least three, potentially four or five, posts about lattice block reduction. The purpose of this series is to give a high level introduction to the most popular algorithms and their analysis, with pointers to the literature for more details. The idea is to start with the obvious – the classic BKZ algorithm. In the next two posts we will look at two lesser known algorithm, which allow to highlight useful tools in lattice reduction. These three posts will focus on provable results. I have not decided how to proceed from there, but I could see the series being extended to topics involving heuristic analyses, practical considerations, and/or a survey of more exotic algorithms that have been considered in the literature.

Target Audience

I will assume that readers of this series are already familiar with basic concepts of lattices, e.g. bases, determinants, successive minima, Minkowski’s bound, Gram-Schmidt orthogonalization, dual lattices and dual bases, etc. If any of these concepts seem new to you, there are great resources to familiarize yourself with them first (see e.g. lecture notes by Daniele, Oded, Daniel/Léo). It will probably help if you are familiar with the LLL algorithm (also covered in aforementioned notes), but I’ll try to phrase everything so it is understandable even if if you aren’t.

Ok, so let’s get started. Before we look at BKZ in particular, first some comments about lattice block reduction in general.

The Basics

The Goal

Why would anyone use block reduction? There are (at least) two reasons.

1) Block reduction allows you to find short vectors in a lattice. Recall that finding the shortest vector in a lattice (i.e. solving SVP) is really hard (as far as we know, this takes at least \(2^{\Omega(n)}\) time or even \(n^{\Omega(n)}\) if you are not willing to also spend exponential amounts of memory). On the other hand, finding somewhat short vectors that are longer than the shortest vector by “only” an exponential factor is really easy (see LLL). So what do you do if you need something that is shorter than what LLL gives you, but you don’t have enough time to actually find the shortest vector? (This situation arises practically every time you use lattice reduction for cryptanalysis.) You can try to find something in between and hope that it doesn’t take as long. This is where lattice reduction comes in: it gives you a smooth trade-off between the two settings. It is worth mentioning that when it comes to approximation algorithms, block reduction is essentially the only game in town, i.e. there are, as far as I know, no non-trivial approximation algorithms that cannot be viewed as block reduction. (In fact, this is related to an open problem that Noah stated during the program: to come up with a non-trivial approximation algorithm that does not rely on a subroutine to find the shortest lattice vector in smaller dimensions.) The only exception to this are quantum algorithms that are able to find subexponential approximations in polynomial time in lattices with certain (cryptographically highly relevant) structure (see [CDPR16] and follow up work).

2) Block reduction actually gives you more than just short vectors. It gives you guarantees on the “quality” of the basis. What do we mean by the quality of the basis? Consider the Gram-Schmidt vectors \({\mathbf{b}}_i^*\) (GSO vectors) associated to a lattice basis \({\mathbf{B}}\). What we want is that the length of these Gram-Schmidt vectors (the GSO norms) does not drop off too quickly. The reason why this is a useful measure of quality for lattice bases is that it gives a sense of how orthogonal the basis vectors are: conditioned on being bases of the same lattice, the less accentuated the drop off in the GSO vectors, the more orthogonal the basis, and the more useful this basis is to solve several problems in a lattice. In fact, recall that the product of the GSO norms is equal to the determinant of the lattice and thus remains constant. Accordingly, if the GSO norms do not drop off too quickly, the first vector can be shown to be relatively short. So by analyzing the quality of the basis that block reduction achieves, a guarantee on the length of the first vector comes for free (see goal 1)). If you are familiar with the analysis of LLL, this should not come as a surprise to you.

Tools

In order to ensure that the GSO norms do not drop off to quickly, it seems useful to be able to reduce them locally. To this end, we will work with projected lattice blocks (this is where the term “block” in block reduction comes from). More formally, given a basis \({\mathbf{B}}\) we will consider the block \({\mathbf{B}}_{[i,j]}\) for \(i < j\) as the basis formed by the basis vectors \({\mathbf{b}}_i, {\mathbf{b}}_{i+1}, \dots, {\mathbf{b}}_{j}\) projected orthogonally to the first \(i-1\) basis vectors. So \({\mathbf{B}}_{[i,j]}\) is a basis for the lattice given by the sublattice formed by \({\mathbf{b}}_1, {\mathbf{b}}_{2}, \dots, {\mathbf{b}}_{j}\) projected onto the orthogonal subspace of the vectors \({\mathbf{b}}_1, {\mathbf{b}}_{2}, \dots, {\mathbf{b}}_{i-1}\). Notice that the first vector of \({\mathbf{B}}_{[i,j]}\) is exactly \({\mathbf{b}}^*_i\) – the \(i\)-th GSO vector. Another way to view this is to consider the QR-factorization of \({\mathbf{B}} = {\mathbf{Q}} {\mathbf{R}}\), where \({\mathbf{B}}\) is the matrix whose columns are the basis vectors \({\mathbf{b}}_i\). Since \({\mathbf{Q}}\) is orthonormal, it represents a rotation of the lattice and we can consider the lattice generated by the columns of \({\mathbf{R}}\) instead, which is an upper triangular matrix. For an upper triangular basis, the projection of a basis vector orthogonal to the previous basis vectors simply results in dropping the first entries from the vector. So considering a projected block \({\mathbf{R}}_{i,j}\) is simply to consider the square submatrix of \({\mathbf{R}}\) consisting of the rows and columns with index \(k\) between \(i \leq k \leq j\).

Now we need a tool that allows us to control these GSO vectors, which we view as the first basis vectors in projected sublattices. For this, we will fall back to algorithms that solve SVP. Recall that this is very expensive, so we will not call this on the basis \({\mathbf{B}}\) but rather on the projected blocks \({\mathbf{B}}_{[i,j]}\), where we ensure that the dimension \(k = j-i+1\) of the lattice generated by this projected block is not too large. In fact, the maximum dimension \(k\) that we call the SVP algorithm on will control the time/quality trade-off achieved by our block reduction algorithms and is usually denoted by the block size. So we will assume that we have access to such an SVP algorithm. Actually, we will assume something slightly stronger: we will assume access to a subroutine that takes as input the basis \({\mathbf{B}}\) and indices \(i,j\) and outputs a basis \({\mathbf{C}}\) such that

  • the lattice generated by the basis remains the same

  • the first \(i-1\) and the last vectors starting from \(j+1\) remain unchanged

  • the projected block \({\mathbf{C}}_{[i,j]}\) is SVP reduced, meaning that \({\mathbf{c}}^*_i\) is the shortest vector in the lattice generated by \({\mathbf{C}}_{[i,j]}\). Additionally, if \({\mathbf{B}}_{[i,j]}\) is already SVP reduced, we assume that the basis \({\mathbf{B}}\) is left unchanged.

We will call an algorithm that achieves this an SVP oracle. Such an oracle can be implemented given any algorithm that solves SVP (for arbitrary lattices). The technical detail of filling in the gap is left as homework to the reader.

Effect of a call to the SVP oracle. GSO log norms of the input in black, of the output in red. Note that the sum of the GSO log norms is a constant, so reducing the first vector, increases the (average of the) remaining vectors.

For the analysis we need to know what such an SVP oracle buys us. This is where Minkowski’s theorem comes in: we know that for any \(n\)-dimensional lattice \(\Lambda\) we have \(\lambda_1(\Lambda) \leq \sqrt{\gamma_n} \det(\Lambda)^{1/n}\) (where \(\lambda_1(\Lambda)\) is the length of the shortest vector in \(\Lambda\) and \(\gamma_n = \Theta(n)\) is Hermite’s constant). This tells us that after we’ve applied the SVP oracle to a projected block \({\mathbf{B}}_{[i,i+k-1]}\), we have \[\|{\mathbf{b}}^*_i \| \leq \sqrt{\gamma_{k}} \left(\prod_{j = i}^{i+k-1} \|{\mathbf{b}}_j^* \| \right)^{1/k}.\] Almost all of the analyses of block reduction algorithms, at least in terms of their output quality, rely on this single inequality.

Disclaimer

Before we finally get to talk about BKZ, I want to remark that throughout this series I will punt on a technical (but very important) topic: the number of arithmetic operations (outside of the oracle calls) and the size of the numbers. The number of arithmetic operations is usually not a problem, since it will be dominated by the calls to the SVP oracle. We will only compute projections of sublattices corresponding to projected blocks as described above to pass them to the oracle, which can be done efficiently using the Gram-Schmidt orthogonalization. The size of the numbers is a more delicate issue. We need to ensure that the required precision for these projections does not explode somehow. This is usually addressed by interleaving the calls to the SVP oracle with calls to LLL. If you are familiar with the LLL algorithm, it should be intuitive that this allows to control the size of the number. For a clean example of how this can be handled, we refer to e.g. [GN08a]. So, in summary, we will measure the running time of our algorithms thoughout simply in the number of calls to the SVP oracle.

BKZ

Schnorr [S87] introduced the concept of BKZ reduction in the 80’s as a generalization of LLL. The first version of the BKZ algorithm as we consider it today was proposed by Schnorr and Euchner [SE94] a few years later. With our setup above, the algorithm can be described in a very simple way. Let \({\mathbf{B}}\) be a lattice basis of an \(n\)-dimensional lattice and \(k\) be the block size. Recall that this is a parameter that will determine the time/quality trade-off as we shall see in the analysis. We start by calling the SVP oracle on the first block \({\mathbf{B}}_{[1,k]}\) of size \(k\). Once this block is SVP reduced, we shift our attention to the next block \({\mathbf{B}}_{[2,k+1]}\) and call the oracle on that. Notice that SVP reduction of \({\mathbf{B}}_{[2,k+1]}\) may change the lattice generated by \({\mathbf{B}}_{[1,k]}\) and \({\mathbf{b}}_1\) may not be the shortest vector in the first block anymore, i.e. it can potentially be reduced even further. However, instead of going back and fixing that, we will simply leave this as a problem to “future us”. For now, we continue in this fashion until we reach the end of the basis, i.e. until we called the oracle on \({\mathbf{B}}_{n-k,n}\). Note that so far this can be viewed as considering a constant sized window moving from the start of the basis to the end and reducing the first vector of the projected block in this window as much as possible using the oracle. Once we have reached the end of the basis, we start reducing the window size, i.e. we call the oracle on \({\mathbf{B}}_{n-k+1,n}\), then on \({\mathbf{B}}_{n-k+2,n}\), etc. This whole process is called a BKZ tour.

Now that we have finished a tour, it is time to go back and fix the blocks that are not SVP reduced anymore. We do this simply by running another tour. Again, if the second tour modified the basis, there is no guarantee that all the blocks are SVP redcued. So we simply repeat, and repeat, and … you get the idea. We run as many tours as required until the basis does not change anymore. That’s it. If this looks familiar to you, that’s not a coincidence: if we plug in \(k=2\) as our block size, we obtain (a version of) LLL! So BKZ is a proper generalization of LLL.

BKZ in one picture: apply the SVP oracle to the projected blocks from start to finish and when you reach the end, repeat.

The obvious questions now are: what can we expect from the output? And how long does it take?

The Good

We will now take a closer look at the approximation factor achieved by BKZ. If you want to follow this analysis along, you might want to get out pen and paper. Otherwise, feel free to trust me on the calculations (I wouldn’t!) and/or jump ahead to the end of this section for the result (no spoilers!). Let’s assume for now that the BKZ algorithm terminates. If it does, we know that the projected block \({\mathbf{B}}_{[i, i+k-1]}\) is SVP reduced for every \(i \in [1,\dots,n-k+1]\). This means that we have \[\|{\mathbf{b}}^*_i \|^k \leq \gamma_{k}^{k/2} \prod_{j = i}^{i+k-1} \|{\mathbf{b}}_j^* \|\] for all these \(n-k+1\) values of \(i\). Multiplying all of these inequalities and canceling terms gives the inequality \[\|{\mathbf{b}}^*_1 \|^{k-1}\|{\mathbf{b}}^*_2 \|^{k-2} \dots \|{\mathbf{b}}^*_{k-1} \| \leq \gamma_{k}^{\frac{(n-k+1)k}{2}} \|{\mathbf{b}}_{n-k+2}^* \|^{k-1} \|{\mathbf{b}}_{n-k+3}^* \|^{k-2} \dots \|{\mathbf{b}}_{n}^* \|.\] Now we make two more observations: 1) not only is \({\mathbf{B}}_{[1, k]}\) SVP reduced, but so is \({\mathbf{B}}_{[1, i]}\) for every \(i < k\). (Why? Think about it for 2 seconds!) This means we can multiply the inequalities \[\|{\mathbf{b}}^*_1 \|^i \leq \gamma_{i}^{i/2} \prod_{j = 1}^{i} \|{\mathbf{b}}_j^* \|\] for all \(i \in [2,k-1]\) together with the trivial inequality \(\|{\mathbf{b}}^*_1 \| \leq \|{\mathbf{b}}^*_1 \|\), which gives \[\|{\mathbf{b}}^*_1 \|^{\frac{k(k-1)}{2}} \leq \left(\prod_{i = 2}^{k-1} \gamma_{i}^{i/2} \right) \prod_{i = 1}^{k-1} \|{\mathbf{b}}_i^* \|^{k-1}\] Now we use the fact that \(\gamma_k^k \geq \gamma_i^i\) for all \(i \leq k\) (Why? Homework!) and combine with our long inequality above to get \[\|{\mathbf{b}}^*_1 \|^{\frac{k(k-1)}{2}} \leq \gamma_k^{\frac{k(n-1)}{2}} \|{\mathbf{b}}_{n-k+2}^* \|^{k-1} \|{\mathbf{b}}_{n-k+3}^* \|^{k-2} \dots \|{\mathbf{b}}_{n}^* \|.\] (I’m aware that this is a lengthy calculation for a blog post, but we’re almost there, so bear with me. It’s worth it!)

We now use one final observation, which is a pretty common trick in lattice algorithms: w.l.o.g. assume that for some shortest vector \({\mathbf{v}}\) in our lattice its projection orthogonal to the first \(n-1\) basis vectors is non-zero (if it is zero for all of the shortest vectors, simply drop the last vector from the basis, the result is still BKZ reduced, so use induction). Then we must have that \(\lambda_1 = \| {\mathbf{v}} \| \geq \|{\mathbf{b}}_i^* \|\) for all \(i \in [n-k+2, \dots, n]\), since otherwise the projected block \({\mathbf{B}}_{i,n}\) would not be SVP reduced. This means, we have \(\lambda_1 \geq \max_{i \in [n-k+2, \dots, n]} \|{\mathbf{b}}_i^* \|\). This is the final puzzle piece to get our approximation bound: \[\|{\mathbf{b}}^*_1 \| \leq \gamma_{k}^{\frac{n-1}{k-1}} \lambda_1.\] Note that this analysis (dating back to Schnorr [S94]) is reminiscent of the analysis of LLL and if we plug in \(k=2\), we get exactly what we’d expect from LLL. Though we do note a gap in the other extreme: if we plug in \(k=n\), we know that the approximation factor is \(1\) (we are solving SVP in the entire lattice), but the bound above yields a factor \(\gamma_n = \Theta(n)\).

The Bad

Now that we’ve looked at the output quality of the basis, let’s see what we can say about the running time (recall that our focus is on the number of calls to the SVP oracle). The short answer is: not much and that’s very unfortunate. Ideally, we’d want a bound on the number of SVP calls that is polynomial in \(n\) and \(k\). This would mean that the overall running time for large \(k\) is dominated by the running time of the SVP oracle in dimension \(k\) and the block size would give us exactly the expected trade-off. However, an LLL style analysis has so far only yielded a bound on the number of tours which is \(O(k^n)\) [HPS11, Appendix]. This is quite bad – for large \(k\) the number of calls will be the dominating factor in the running time.

The Ugly

Recall that the analysis of LLL does not only provide a bound on the approximation factor, but also on the Hermite factor, i.e. on the ratio of \(\| {\mathbf{b}}_1\|/\det(\Lambda)^{1/n}\). Since an LLL-style analysis worked out nicely for the approximation factor of BKZ, it stands to reason that a similar analysis should yield a similar bound for BKZ. By extrapolating from LLL, one could expect a bound along the lines of \(\| {\mathbf{b}}_1\|/\det(\Lambda)^{1/n} \leq \gamma_{k}^{n/2k}\) (note the square root improvement w.r.t. the trivial bound obtained from the approximation factor). And, in fact, a bound of \(\gamma_{k}^{\frac{n-1}{2(k-1)} + 1}\) has been claimed in [GN08b] but without proof (as pointed out in [HPS11]) and it is not clear, how one would prove this. ([GN08b] claims that one can use a similar argument as we did for the approximation factor, but I don’t see it.)

The Rescue

So it seems different techniques are necessary to complete the analysis of BKZ. The work of [HPS11] introduced such a new technique based on the analysis of dynamical systems. This work applied the technique successfully to BKZ, but the analysis is quite involved. What it shows is that one can terminate BKZ after a polynomial number of tours and still get a guarantee on the output quality, which is very close to the conjectured bound on the Hermite factor above. (Caveat: Technically, [HPS11] only showed this result for a slight variant of BKZ, but the difference to the standard BKZ algorithm only lies in the scope of the interleaving LLL applications, which is something that we glossed over above.) This is in line with experimental studies [SE94,GN08b,MW16], which show that BKZ produces high quality bases after a few tours already.

We will revisit this approach when considering a different block reduction variant, SDBKZ, where the analysis is much cleaner. As a teaser for the next post though, recall that BKZ can be viewed as a generalization of LLL (which corresponds to BKZ with block size \(k=2\)). Since the analysis of LLL did not carry entirely to BKZ, one could wonder if there is a different generalization of LLL such that an LLL-style analysis also generalizes naturally. The answer to this is yes, and we will consider such an algorithm in the next post.

  • [CDPR16] Cramer, Ducas, Peikert, Regev. Recovering short generators of principal ideals in cyclotomic rings. EUROCRYPT 2016
  • [GN08a] Gama, Nguyen. Finding short lattice vectors within Mordell’s inequality. STOC 2008
  • [GN08b] Gama, Nguyen. Predicting lattice reduction. EUROCRYPT 2008
  • [HPS11] Hanrot, Pujol, Stehlé. Analyzing blockwise lattice algorithms using dynamical systems. CRYPTO 2011
  • [MW16] Micciancio, Walter. Practical, predictable lattice basis reduction. EUROCRYPT 2016
  • [SE94] Schnorr, Euchner. Lattice basis reduction: Improved practical algorithms and solving subset sum problems. Mathematical Programming 1994
  • [S87] Schnorr. A hierarchy of polynomial time lattice basis reduction algorithms. Theoretical Computer Science 1987
  • [S94] Schnorr. Block reduced lattice bases and successive minima. Combinatorics, Probability and Computing 1994