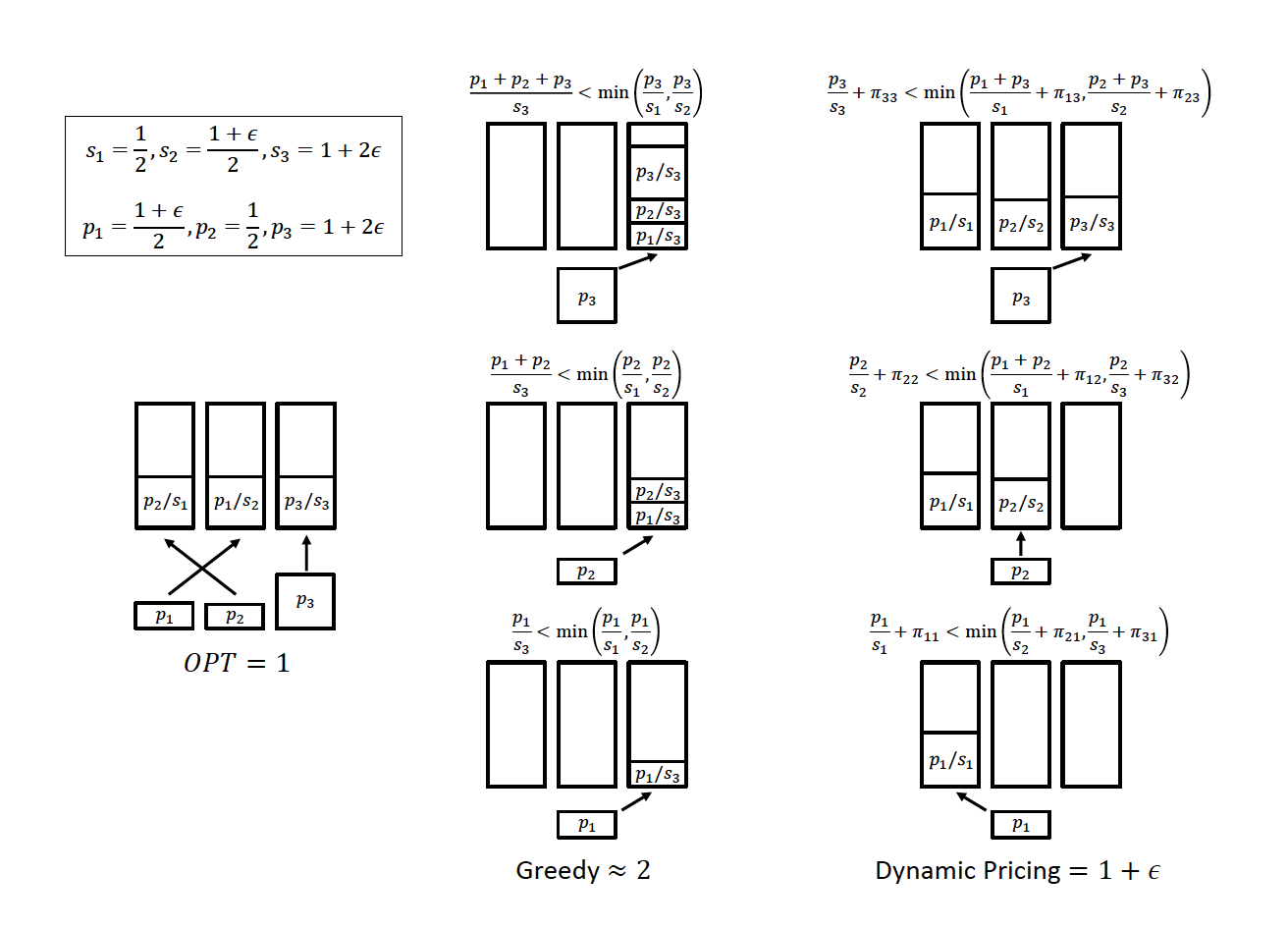
This is the first entry in a (planned) series of at least three, potentially four or five, posts about lattice block reduction. The purpose of this series is to give a high level introduction to the most popular algorithms and their analysis, with pointers to the literature for more details. The idea is to start with the obvious – the classic BKZ algorithm. In the next two posts we will look at two lesser known algorithm, which allow to highlight useful tools in lattice reduction. These three posts will focus on provable results. I have not decided how to proceed from there, but I could see the series being extended to topics involving heuristic analyses, practical considerations, and/or a survey of more exotic algorithms that have been considered in the literature.
Target Audience
I will assume that readers of this series are already familiar with basic concepts of lattices, e.g. bases, determinants, successive minima, Minkowski’s bound, Gram-Schmidt orthogonalization, dual lattices and dual bases, etc. If any of these concepts seem new to you, there are great resources to familiarize yourself with them first (see e.g. lecture notes by Daniele, Oded, Daniel/Léo). It will probably help if you are familiar with the LLL algorithm (also covered in aforementioned notes), but I’ll try to phrase everything so it is understandable even if if you aren’t.
Ok, so let’s get started. Before we look at BKZ in particular, first some comments about lattice block reduction in general.
The Basics
The Goal
Why would anyone use block reduction? There are (at least) two reasons.
1) Block reduction allows you to find short vectors in a lattice. Recall that finding the shortest vector in a lattice (i.e. solving SVP) is really hard (as far as we know, this takes at least \(2^{\Omega(n)}\) time or even \(n^{\Omega(n)}\) if you are not willing to also spend exponential amounts of memory). On the other hand, finding somewhat short vectors that are longer than the shortest vector by “only” an exponential factor is really easy (see LLL). So what do you do if you need something that is shorter than what LLL gives you, but you don’t have enough time to actually find the shortest vector? (This situation arises practically every time you use lattice reduction for cryptanalysis.) You can try to find something in between and hope that it doesn’t take as long. This is where lattice reduction comes in: it gives you a smooth trade-off between the two settings. It is worth mentioning that when it comes to approximation algorithms, block reduction is essentially the only game in town, i.e. there are, as far as I know, no non-trivial approximation algorithms that cannot be viewed as block reduction. (In fact, this is related to an open problem that Noah stated during the program: to come up with a non-trivial approximation algorithm that does not rely on a subroutine to find the shortest lattice vector in smaller dimensions.) The only exception to this are quantum algorithms that are able to find subexponential approximations in polynomial time in lattices with certain (cryptographically highly relevant) structure (see [CDPR16] and follow up work).
2) Block reduction actually gives you more than just short vectors. It gives you guarantees on the “quality” of the basis. What do we mean by the quality of the basis? Consider the Gram-Schmidt vectors \({\mathbf{b}}_i^*\) (GSO vectors) associated to a lattice basis \({\mathbf{B}}\). What we want is that the length of these Gram-Schmidt vectors (the GSO norms) does not drop off too quickly. The reason why this is a useful measure of quality for lattice bases is that it gives a sense of how orthogonal the basis vectors are: conditioned on being bases of the same lattice, the less accentuated the drop off in the GSO vectors, the more orthogonal the basis, and the more useful this basis is to solve several problems in a lattice. In fact, recall that the product of the GSO norms is equal to the determinant of the lattice and thus remains constant. Accordingly, if the GSO norms do not drop off too quickly, the first vector can be shown to be relatively short. So by analyzing the quality of the basis that block reduction achieves, a guarantee on the length of the first vector comes for free (see goal 1)). If you are familiar with the analysis of LLL, this should not come as a surprise to you.
Tools
In order to ensure that the GSO norms do not drop off to quickly, it seems useful to be able to reduce them locally. To this end, we will work with projected lattice blocks (this is where the term “block” in block reduction comes from). More formally, given a basis \({\mathbf{B}}\) we will consider the block \({\mathbf{B}}_{[i,j]}\) for \(i < j\) as the basis formed by the basis vectors \({\mathbf{b}}_i, {\mathbf{b}}_{i+1}, \dots, {\mathbf{b}}_{j}\) projected orthogonally to the first \(i-1\) basis vectors. So \({\mathbf{B}}_{[i,j]}\) is a basis for the lattice given by the sublattice formed by \({\mathbf{b}}_1, {\mathbf{b}}_{2}, \dots, {\mathbf{b}}_{j}\) projected onto the orthogonal subspace of the vectors \({\mathbf{b}}_1, {\mathbf{b}}_{2}, \dots, {\mathbf{b}}_{i-1}\). Notice that the first vector of \({\mathbf{B}}_{[i,j]}\) is exactly \({\mathbf{b}}^*_i\) – the \(i\)-th GSO vector. Another way to view this is to consider the QR-factorization of \({\mathbf{B}} = {\mathbf{Q}} {\mathbf{R}}\), where \({\mathbf{B}}\) is the matrix whose columns are the basis vectors \({\mathbf{b}}_i\). Since \({\mathbf{Q}}\) is orthonormal, it represents a rotation of the lattice and we can consider the lattice generated by the columns of \({\mathbf{R}}\) instead, which is an upper triangular matrix. For an upper triangular basis, the projection of a basis vector orthogonal to the previous basis vectors simply results in dropping the first entries from the vector. So considering a projected block \({\mathbf{R}}_{i,j}\) is simply to consider the square submatrix of \({\mathbf{R}}\) consisting of the rows and columns with index \(k\) between \(i \leq k \leq j\).
Now we need a tool that allows us to control these GSO vectors, which we view as the first basis vectors in projected sublattices. For this, we will fall back to algorithms that solve SVP. Recall that this is very expensive, so we will not call this on the basis \({\mathbf{B}}\) but rather on the projected blocks \({\mathbf{B}}_{[i,j]}\), where we ensure that the dimension \(k = j-i+1\) of the lattice generated by this projected block is not too large. In fact, the maximum dimension \(k\) that we call the SVP algorithm on will control the time/quality trade-off achieved by our block reduction algorithms and is usually denoted by the block size. So we will assume that we have access to such an SVP algorithm. Actually, we will assume something slightly stronger: we will assume access to a subroutine that takes as input the basis \({\mathbf{B}}\) and indices \(i,j\) and outputs a basis \({\mathbf{C}}\) such that
the lattice generated by the basis remains the same
the first \(i-1\) and the last vectors starting from \(j+1\) remain unchanged
the projected block \({\mathbf{C}}_{[i,j]}\) is SVP reduced, meaning that \({\mathbf{c}}^*_i\) is the shortest vector in the lattice generated by \({\mathbf{C}}_{[i,j]}\). Additionally, if \({\mathbf{B}}_{[i,j]}\) is already SVP reduced, we assume that the basis \({\mathbf{B}}\) is left unchanged.
We will call an algorithm that achieves this an SVP oracle. Such an oracle can be implemented given any algorithm that solves SVP (for arbitrary lattices). The technical detail of filling in the gap is left as homework to the reader.
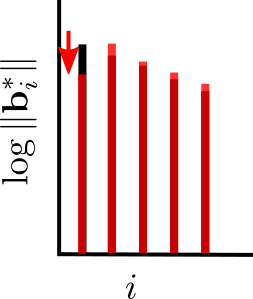
For the analysis we need to know what such an SVP oracle buys us. This is where Minkowski’s theorem comes in: we know that for any \(n\)-dimensional lattice \(\Lambda\) we have \(\lambda_1(\Lambda) \leq \sqrt{\gamma_n} \det(\Lambda)^{1/n}\) (where \(\lambda_1(\Lambda)\) is the length of the shortest vector in \(\Lambda\) and \(\gamma_n = \Theta(n)\) is Hermite’s constant). This tells us that after we’ve applied the SVP oracle to a projected block \({\mathbf{B}}_{[i,i+k-1]}\), we have \[\|{\mathbf{b}}^*_i \| \leq \sqrt{\gamma_{k}} \left(\prod_{j = i}^{i+k-1} \|{\mathbf{b}}_j^* \| \right)^{1/k}.\] Almost all of the analyses of block reduction algorithms, at least in terms of their output quality, rely on this single inequality.
Disclaimer
Before we finally get to talk about BKZ, I want to remark that throughout this series I will punt on a technical (but very important) topic: the number of arithmetic operations (outside of the oracle calls) and the size of the numbers. The number of arithmetic operations is usually not a problem, since it will be dominated by the calls to the SVP oracle. We will only compute projections of sublattices corresponding to projected blocks as described above to pass them to the oracle, which can be done efficiently using the Gram-Schmidt orthogonalization. The size of the numbers is a more delicate issue. We need to ensure that the required precision for these projections does not explode somehow. This is usually addressed by interleaving the calls to the SVP oracle with calls to LLL. If you are familiar with the LLL algorithm, it should be intuitive that this allows to control the size of the number. For a clean example of how this can be handled, we refer to e.g. [GN08a]. So, in summary, we will measure the running time of our algorithms thoughout simply in the number of calls to the SVP oracle.
BKZ
Schnorr [S87] introduced the concept of BKZ reduction in the 80’s as a generalization of LLL. The first version of the BKZ algorithm as we consider it today was proposed by Schnorr and Euchner [SE94] a few years later. With our setup above, the algorithm can be described in a very simple way. Let \({\mathbf{B}}\) be a lattice basis of an \(n\)-dimensional lattice and \(k\) be the block size. Recall that this is a parameter that will determine the time/quality trade-off as we shall see in the analysis. We start by calling the SVP oracle on the first block \({\mathbf{B}}_{[1,k]}\) of size \(k\). Once this block is SVP reduced, we shift our attention to the next block \({\mathbf{B}}_{[2,k+1]}\) and call the oracle on that. Notice that SVP reduction of \({\mathbf{B}}_{[2,k+1]}\) may change the lattice generated by \({\mathbf{B}}_{[1,k]}\) and \({\mathbf{b}}_1\) may not be the shortest vector in the first block anymore, i.e. it can potentially be reduced even further. However, instead of going back and fixing that, we will simply leave this as a problem to “future us”. For now, we continue in this fashion until we reach the end of the basis, i.e. until we called the oracle on \({\mathbf{B}}_{n-k,n}\). Note that so far this can be viewed as considering a constant sized window moving from the start of the basis to the end and reducing the first vector of the projected block in this window as much as possible using the oracle. Once we have reached the end of the basis, we start reducing the window size, i.e. we call the oracle on \({\mathbf{B}}_{n-k+1,n}\), then on \({\mathbf{B}}_{n-k+2,n}\), etc. This whole process is called a BKZ tour.
Now that we have finished a tour, it is time to go back and fix the blocks that are not SVP reduced anymore. We do this simply by running another tour. Again, if the second tour modified the basis, there is no guarantee that all the blocks are SVP redcued. So we simply repeat, and repeat, and … you get the idea. We run as many tours as required until the basis does not change anymore. That’s it. If this looks familiar to you, that’s not a coincidence: if we plug in \(k=2\) as our block size, we obtain (a version of) LLL! So BKZ is a proper generalization of LLL.

The obvious questions now are: what can we expect from the output? And how long does it take?
The Good
We will now take a closer look at the approximation factor achieved by BKZ. If you want to follow this analysis along, you might want to get out pen and paper. Otherwise, feel free to trust me on the calculations (I wouldn’t!) and/or jump ahead to the end of this section for the result (no spoilers!). Let’s assume for now that the BKZ algorithm terminates. If it does, we know that the projected block \({\mathbf{B}}_{[i, i+k-1]}\) is SVP reduced for every \(i \in [1,\dots,n-k+1]\). This means that we have \[\|{\mathbf{b}}^*_i \|^k \leq \gamma_{k}^{k/2} \prod_{j = i}^{i+k-1} \|{\mathbf{b}}_j^* \|\] for all these \(n-k+1\) values of \(i\). Multiplying all of these inequalities and canceling terms gives the inequality \[\|{\mathbf{b}}^*_1 \|^{k-1}\|{\mathbf{b}}^*_2 \|^{k-2} \dots \|{\mathbf{b}}^*_{k-1} \| \leq \gamma_{k}^{\frac{(n-k+1)k}{2}} \|{\mathbf{b}}_{n-k+2}^* \|^{k-1} \|{\mathbf{b}}_{n-k+3}^* \|^{k-2} \dots \|{\mathbf{b}}_{n}^* \|.\] Now we make two more observations: 1) not only is \({\mathbf{B}}_{[1, k]}\) SVP reduced, but so is \({\mathbf{B}}_{[1, i]}\) for every \(i < k\). (Why? Think about it for 2 seconds!) This means we can multiply the inequalities \[\|{\mathbf{b}}^*_1 \|^i \leq \gamma_{i}^{i/2} \prod_{j = 1}^{i} \|{\mathbf{b}}_j^* \|\] for all \(i \in [2,k-1]\) together with the trivial inequality \(\|{\mathbf{b}}^*_1 \| \leq \|{\mathbf{b}}^*_1 \|\), which gives \[\|{\mathbf{b}}^*_1 \|^{\frac{k(k-1)}{2}} \leq \left(\prod_{i = 2}^{k-1} \gamma_{i}^{i/2} \right) \prod_{i = 1}^{k-1} \|{\mathbf{b}}_i^* \|^{k-1}\] Now we use the fact that \(\gamma_k^k \geq \gamma_i^i\) for all \(i \leq k\) (Why? Homework!) and combine with our long inequality above to get \[\|{\mathbf{b}}^*_1 \|^{\frac{k(k-1)}{2}} \leq \gamma_k^{\frac{k(n-1)}{2}} \|{\mathbf{b}}_{n-k+2}^* \|^{k-1} \|{\mathbf{b}}_{n-k+3}^* \|^{k-2} \dots \|{\mathbf{b}}_{n}^* \|.\] (I’m aware that this is a lengthy calculation for a blog post, but we’re almost there, so bear with me. It’s worth it!)
We now use one final observation, which is a pretty common trick in lattice algorithms: w.l.o.g. assume that for some shortest vector \({\mathbf{v}}\) in our lattice its projection orthogonal to the first \(n-1\) basis vectors is non-zero (if it is zero for all of the shortest vectors, simply drop the last vector from the basis, the result is still BKZ reduced, so use induction). Then we must have that \(\lambda_1 = \| {\mathbf{v}} \| \geq \|{\mathbf{b}}_i^* \|\) for all \(i \in [n-k+2, \dots, n]\), since otherwise the projected block \({\mathbf{B}}_{i,n}\) would not be SVP reduced. This means, we have \(\lambda_1 \geq \max_{i \in [n-k+2, \dots, n]} \|{\mathbf{b}}_i^* \|\). This is the final puzzle piece to get our approximation bound: \[\|{\mathbf{b}}^*_1 \| \leq \gamma_{k}^{\frac{n-1}{k-1}} \lambda_1.\] Note that this analysis (dating back to Schnorr [S94]) is reminiscent of the analysis of LLL and if we plug in \(k=2\), we get exactly what we’d expect from LLL. Though we do note a gap in the other extreme: if we plug in \(k=n\), we know that the approximation factor is \(1\) (we are solving SVP in the entire lattice), but the bound above yields a factor \(\gamma_n = \Theta(n)\).
The Bad
Now that we’ve looked at the output quality of the basis, let’s see what we can say about the running time (recall that our focus is on the number of calls to the SVP oracle). The short answer is: not much and that’s very unfortunate. Ideally, we’d want a bound on the number of SVP calls that is polynomial in \(n\) and \(k\). This would mean that the overall running time for large \(k\) is dominated by the running time of the SVP oracle in dimension \(k\) and the block size would give us exactly the expected trade-off. However, an LLL style analysis has so far only yielded a bound on the number of tours which is \(O(k^n)\) [HPS11, Appendix]. This is quite bad – for large \(k\) the number of calls will be the dominating factor in the running time.
The Ugly
Recall that the analysis of LLL does not only provide a bound on the approximation factor, but also on the Hermite factor, i.e. on the ratio of \(\| {\mathbf{b}}_1\|/\det(\Lambda)^{1/n}\). Since an LLL-style analysis worked out nicely for the approximation factor of BKZ, it stands to reason that a similar analysis should yield a similar bound for BKZ. By extrapolating from LLL, one could expect a bound along the lines of \(\| {\mathbf{b}}_1\|/\det(\Lambda)^{1/n} \leq \gamma_{k}^{n/2k}\) (note the square root improvement w.r.t. the trivial bound obtained from the approximation factor). And, in fact, a bound of \(\gamma_{k}^{\frac{n-1}{2(k-1)} + 1}\) has been claimed in [GN08b] but without proof (as pointed out in [HPS11]) and it is not clear, how one would prove this. ([GN08b] claims that one can use a similar argument as we did for the approximation factor, but I don’t see it.)
The Rescue
So it seems different techniques are necessary to complete the analysis of BKZ. The work of [HPS11] introduced such a new technique based on the analysis of dynamical systems. This work applied the technique successfully to BKZ, but the analysis is quite involved. What it shows is that one can terminate BKZ after a polynomial number of tours and still get a guarantee on the output quality, which is very close to the conjectured bound on the Hermite factor above. (Caveat: Technically, [HPS11] only showed this result for a slight variant of BKZ, but the difference to the standard BKZ algorithm only lies in the scope of the interleaving LLL applications, which is something that we glossed over above.) This is in line with experimental studies [SE94,GN08b,MW16], which show that BKZ produces high quality bases after a few tours already.
We will revisit this approach when considering a different block reduction variant, SDBKZ, where the analysis is much cleaner. As a teaser for the next post though, recall that BKZ can be viewed as a generalization of LLL (which corresponds to BKZ with block size \(k=2\)). Since the analysis of LLL did not carry entirely to BKZ, one could wonder if there is a different generalization of LLL such that an LLL-style analysis also generalizes naturally. The answer to this is yes, and we will consider such an algorithm in the next post.
- [CDPR16] Cramer, Ducas, Peikert, Regev. Recovering short generators of principal ideals in cyclotomic rings. EUROCRYPT 2016
- [GN08a] Gama, Nguyen. Finding short lattice vectors within Mordell’s inequality. STOC 2008
- [GN08b] Gama, Nguyen. Predicting lattice reduction. EUROCRYPT 2008
- [HPS11] Hanrot, Pujol, Stehlé. Analyzing blockwise lattice algorithms using dynamical systems. CRYPTO 2011
- [MW16] Micciancio, Walter. Practical, predictable lattice basis reduction. EUROCRYPT 2016
- [SE94] Schnorr, Euchner. Lattice basis reduction: Improved practical algorithms and solving subset sum problems. Mathematical Programming 1994
- [S87] Schnorr. A hierarchy of polynomial time lattice basis reduction algorithms. Theoretical Computer Science 1987
- [S94] Schnorr. Block reduced lattice bases and successive minima. Combinatorics, Probability and Computing 1994

 Fitting a model to a collection of observations is one of the quintessential goals of statistics and machine learning. A major recent advance in theoretical machine learning is the development of efficient learning algorithms for various high-dimensional models, including Gaussian mixture models, independent component analysis, and topic models. The Achilles’ heel of these algorithms is the assumption that data is precisely generated from a model of the given type.
Fitting a model to a collection of observations is one of the quintessential goals of statistics and machine learning. A major recent advance in theoretical machine learning is the development of efficient learning algorithms for various high-dimensional models, including Gaussian mixture models, independent component analysis, and topic models. The Achilles’ heel of these algorithms is the assumption that data is precisely generated from a model of the given type.
 Computational complexity theory studies the possibilities and limitations of algorithms. Over the past several decades, we have learned a lot about the possibilities of algorithms. We live today in an algorithmic world, where the ability to reliably and quickly process vast amounts of data is crucial. Along with this social and technological transformation, there have been significant theoretical advances, including the discovery of efficient algorithms for fundamental problems such as linear programming and primality.
Computational complexity theory studies the possibilities and limitations of algorithms. Over the past several decades, we have learned a lot about the possibilities of algorithms. We live today in an algorithmic world, where the ability to reliably and quickly process vast amounts of data is crucial. Along with this social and technological transformation, there have been significant theoretical advances, including the discovery of efficient algorithms for fundamental problems such as linear programming and primality.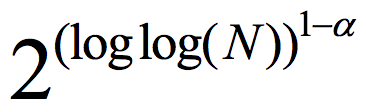 for some constant
for some constant 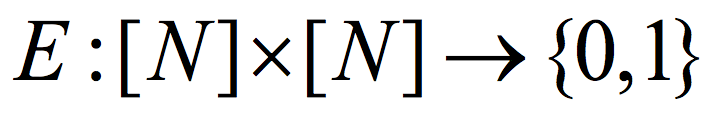 is a (K,ϵ) 2-source extractor if for every two cardinality K subsets
is a (K,ϵ) 2-source extractor if for every two cardinality K subsets 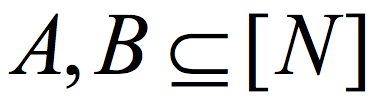 , the distribution E(A,B) (obtained by picking uniformly
, the distribution E(A,B) (obtained by picking uniformly 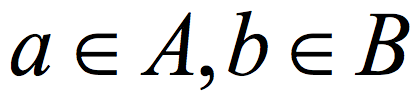 and outputting E(a,b)) is ε close to uniform in the variational distance. Roughly speaking, the Ramsey graph problem is to find a (K, ε) 2-source extractor with any error ε= ε(K) smaller than 1, even allowing error that is exponentially close to 1. In contrast, The CZ construction gives a 2-source extractor with constant error. A 2-source extractor is a basic object of fundamental importance, and the previous best 2-source construction was Bourgain’s extractor, requiring log(K) =
and outputting E(a,b)) is ε close to uniform in the variational distance. Roughly speaking, the Ramsey graph problem is to find a (K, ε) 2-source extractor with any error ε= ε(K) smaller than 1, even allowing error that is exponentially close to 1. In contrast, The CZ construction gives a 2-source extractor with constant error. A 2-source extractor is a basic object of fundamental importance, and the previous best 2-source construction was Bourgain’s extractor, requiring log(K) =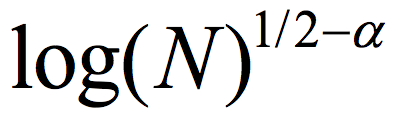 for some small constant α>0. The CZ construction is an exponential improvement over that, requiring only log(K)=polyloglog(N).
for some small constant α>0. The CZ construction is an exponential improvement over that, requiring only log(K)=polyloglog(N).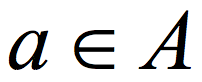 ) with a t non-malleable extractor. I do not want to formally define non-malleability here, but this essentially means that the bits of the encoded string are “almost” t-wise independent, in the sense that except for few “bad” bits, when we look at t bits, they are close to being uniform. The next step in the CZ construction is to use the sample from the second source (
) with a t non-malleable extractor. I do not want to formally define non-malleability here, but this essentially means that the bits of the encoded string are “almost” t-wise independent, in the sense that except for few “bad” bits, when we look at t bits, they are close to being uniform. The next step in the CZ construction is to use the sample from the second source (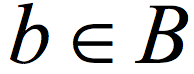 ) to sample a substring of the encoding of a. The sampling is done using an extractor and uses the known relationship between extractors and samplers.
) to sample a substring of the encoding of a. The sampling is done using an extractor and uses the known relationship between extractors and samplers.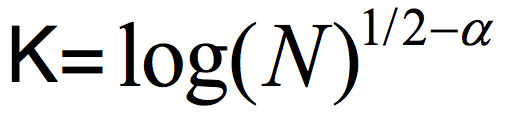 and Raz’ extractor which allows one source to be (almost) arbitrarily weak, but requires the other source to have min-entropy rate above half (the entropy rate is the min-entropy divided by the length of the string). At the Simons Institute program on Pseudorandomness, we were wondering whether the CZ approach that allows both sources to be weak can be somehow modified to give a low-error construction?
and Raz’ extractor which allows one source to be (almost) arbitrarily weak, but requires the other source to have min-entropy rate above half (the entropy rate is the min-entropy divided by the length of the string). At the Simons Institute program on Pseudorandomness, we were wondering whether the CZ approach that allows both sources to be weak can be somehow modified to give a low-error construction?